2023/7/10
イントロダクション
確率プロットは,データが正規分布他の理論分布にしたがっているかどうかを目視で確認してみたいとき有効なグラフです。
とりわけ,ここではデータの正規性を期待した場合の「正規確率プロット」(以下,「Q-Qプロット」)を作図します。もしこの期待が満たされるのであれば,グラフにプロットされるマーカーは一定の勾配をもつ直線状に描かれることになります。
以下,ExcelによるQ-Qプロットの作り方です。ここでは一連の手続きを Excel 2016 で追っています。一部ボタンの配置や名称などが異なる箇所がありますが(この場合,可能であれば当該箇所に明記します),手続きそのものは,「永続ライセンス版」にいうところの Excel 2019, Excel 2013 あるいは Excel 2010 そして,「Microsoft365版」のExcel (本頁更新時点のver.2007)とも基本的には同じです。
なお,下のスイッチで新機能「スピル」に沿った説明に切り替えが可能です(デフォルト:OFF)。

元データ
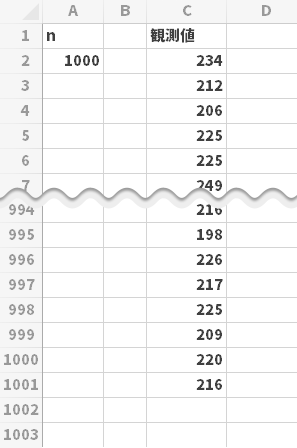
下図上段は,今回の元データです。具体的には,ぶ厚い事典の中ほどに位置する特定の1ページをめがけて,事典の最初から指を滑らせながらぴったり止めようと1000回試行した結果です(ページ数を用紙の枚数に換算)。
下図下段でこのデータの分布をヒストグラムにより可視化し,正規分布曲線(赤線)と重ねてみると,正規分布にしたがっていることがわかります。
このページでは,同様のことをヒストグラムでなくQ-Qプロットでおこないます。以下,その手続きです。

ここにいう「Q-Qプロット」について
その前に目的は違わずとも,グラフとしてのQ-Qプロットには横軸・縦軸が異なるさまざまな書式のものがあります(cf. Google画像検索の結果)。
前提として,ここでは多くのユーザーに利用されている統計処理系「R」に準じた形式をとっていこうと思います。
1 のデータを「R」を通して出力したプレーンなQ-Qプロット[qqnorm()関数による]は,下の図のとおりです(※グレーの囲み文字のみ除く)。すなわちここで描画するQ-Qプロットも同様,横軸には標準正規分布の分位点を,縦軸には観測値をとって,観測値に対する理論分布(ここでは正規分布)上の期待値とを照らしていきたいと思います。

シートに見出しを2つ用意します。
中身は後述しますが,識別できれば何であれかまいません。とりあえず,ここでは%順位Normsinv(%順位)とします。

あえと,このへんでざっくりと,このあとのアウトラインに触れておきます。
グラフを描くために必要なのは,「観測値」列,および「Normsinv(%順位)」列の2つで足るのですが,後者をダイレクトに求めると計算式が長くなってしまうので,何をやっているかを明確にする意図から過程を2つに分割したいと思います。
すなわち「観測値」から「%順位」(パーセンタイル順位)を求め,「%順位」から「Normsinv(%順位)」(標準正規分布と照らした期待値)を求めるといった流れですすめたいと思います。

また,先の方針(Rに準じる)に倣って,「Normsinv(%順位)」列は散布図の横軸に,「観測値」列は同じく縦軸に充てる予定です。

パーセンタイル順位に置き換えてみる
では,具体的に「%順位」列から埋めていきます。ここでは何をやるかというと,観測値の昇順で,百分率での順位づけをおこないます。
見出し直下のセルに下式を入力し,これを表の最下行までコピーします。
- CELL D2=((RANK.EQ(C2,\$C\$2:\$C\$1001,1)+COUNTIF(\$C\$2:C2,C2)-1)-1/2)/\$A\$2
![[セルD2]=((RANK.EQ(C2, \$C\$2:\$C\$1001, 1)+COUNTIF(\$C\$2:C2, C2)-1)-1/2)/\$A\$2](../images/howto/qq-plot/step6.png)
さて,上の長ったらしい式の説明です。
下の図の  線部分は,ざっくり言えば,1 から順に2,3といった感じに一般にいう並びの順位を計算する要素です。そこでさらに話を単純にするため,式の中の
線部分は,ざっくり言えば,1 から順に2,3といった感じに一般にいう並びの順位を計算する要素です。そこでさらに話を単純にするため,式の中の  線部分を「順位」という語で置き換えれば (順位$-1/2$)/$n$ といった式が出来上がります。
線部分を「順位」という語で置き換えれば (順位$-1/2$)/$n$ といった式が出来上がります。
![[数式の構造] =(順位-0.5)/n](../images/howto/qq-plot/step7.svg)
このページのQ-Qプロットの描画法では,「Rに準じる」趣旨から“順位”といったものをこの式 (順位$-1/2$)/$n$ で定義しなおしています。ただし,そうした縛りのない場所では下のような諸式を利用することもあります($\,i\,$: 順位)。
| 1. | $(i-0.375)\,/\,(n+0.25)$ |
| 2. | $(i-0.3)\,/\,(n+0.4)$ |
| 3. | $i\,/\,(n+1)$ |
| 4. | $i\,/\,n$ |
[表の出所] 17.2.4 Probability Plot and Q-Q Plot ―"OriginLab" を一部改変
また,中身がブラックボックスで問題なければ Excel固有のPercentRank系関数も利用できるかと思いますが,Q-Qプロットが主観に依存する視覚的な判断をおこなうものである以上,上記の手法含めどれが優れているのかといった議論は馴染みがたいように感じます。
さて,つづいては,先ほど端折った下図にいう  線部の式です。
線部の式です。
Excelの組み込み関数「Rank.Eq」は,同値の場合同順位で処理します(=欠番が発生します)。こちらも,先に掲げた「Rに準じる」趣旨のもとでは意に沿わないので,CountIf関数で前方にある同値の存在を調べ,それ(ら)を見つけた場合,より後の(ワークシートで言えば下方の)値を下位とする旨の処置を咬ませます(=欠番が発生しません)。
![[RANK.EQのみ]同順位→同値→欠番あり [RANK.EQとCOUNTIFの組み合わせ]同値→先の方を上位に→欠番なし](../images/howto/qq-plot/step9.svg)
その下側確率なら,z分布はどの値を返す?
「Normsinv(%順位)」列に次の式を入力し,表の最下行までコピーします。
- CELL E2=NORM.S.INV(D2)
![[セルE2]=NORM.S.INV(D2)](../images/howto/qq-plot/step10.png)
見出し「Normsinv(%順位)」の直下に次の式を入力します。
- CELL E2=NORM.S.INV(D2:D1001)
![[セルE2]=NORM.S.INV(D2:D1001)](../images/howto/qq-plot/step10-1-spill.png)
「散布図」にプロットして あてはまりを判断する
ここからグラフを描画していきます。
早速,散布図をつくるのに必要な「観測値」および「Normsinv(%順位)」列をいちどに選択して手続きを進めたいところですが,ここでExcelのグラフまわりの仕様として,シートの上でより左側にある列が横軸へと割り振られるといったことに注意する必要があります。何らの準備なくそのままグラフを描きすすめると,当然,当初思い描いたものとは体裁を異にしてしまいます。
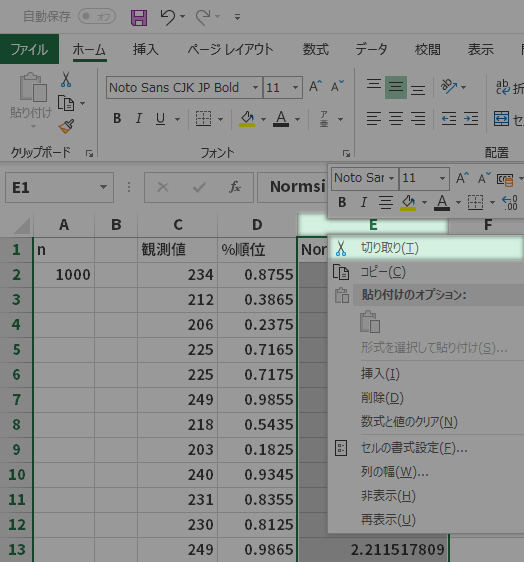
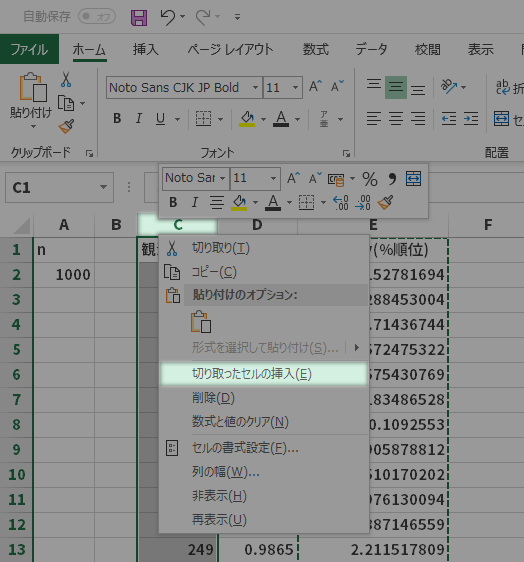
ということで,ここらで仕様に沿うようなかたちつまり「観測値」列と「Normsinv(%順位)」列の位置関係を解決しておくとその後がスムーズです。具体的には,E列を切り取り(下図上段),C列に切り取ったセルの挿入(下図下段)をして対処したいと思います。
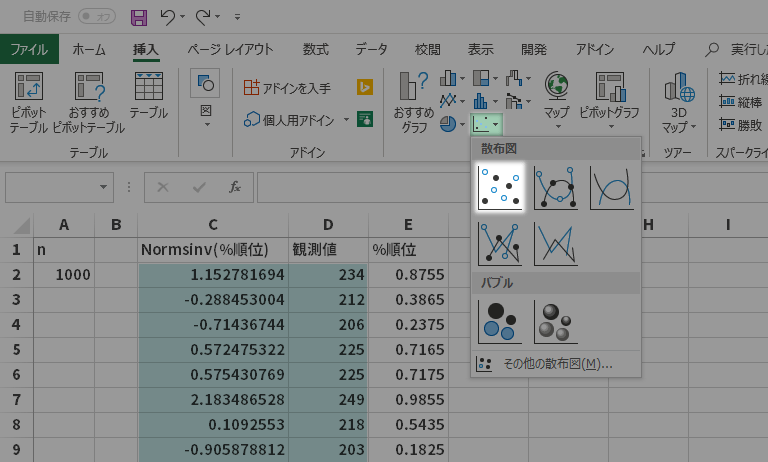
「Normsinv(%順位)」および「観測値」列を選択後,リボンの挿入タブグラフグループにある散布図(X, Y)またはバブルチャートの挿入ボタン散布図ボタンとクリックします。
この操作でグラフ(散布図)がシートの上に出力されます。
DIFFERENT VERSIONS
2010: [挿入]タブ[散布図]ボタン[散布図(マーカーのみ)]ボタン
あ!
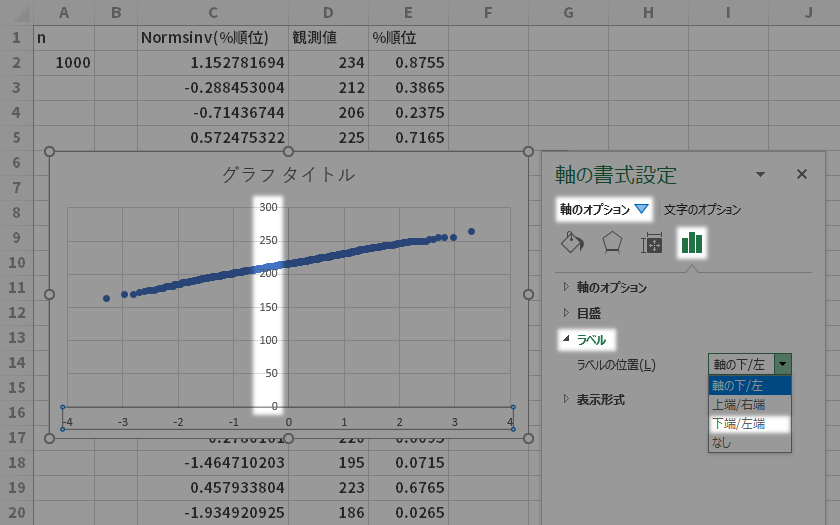
下の図縦軸のラベルがこの位置に据えられましたね。Q-Qプロット的にはどこかハマりがわるいようにも感じるので,これをグラフの左側に寄せ直したいと思います(ユーザーの好みで)。
第1縦軸をアクティブにした状態から,ダブルクリックなどで書式設定ウィンドウを呼び出し,軸のオプショングループ・ラベルのラベルの位置を下端/左端に変更します。
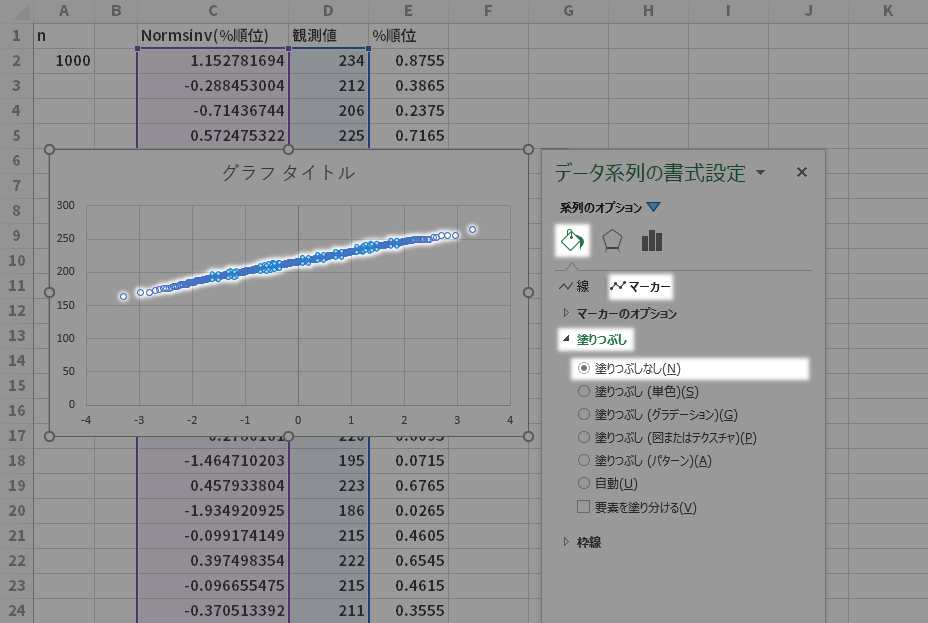
とりわけ$n$がある程度の大きさをもってくると,(正規分布の性質上50パーセンタイル[横軸0]周辺は必然的に密度が濃くなるゆえ)彩色ずみのマーカーではややもすると1本の線のようにも見えてきます。これはいささかのっぺりすぎる印象なので,Rに倣いデフォルトの塗り色を抜いた方が,“密度”を表現するうえでもbetterなような気もします(判断により)。
この場合,この作例でのグラフの系列"系列1"(平たく言えば “グラフ上のマーカー群”)をアクティブにした状態から,(もし書式設定ウィンドウを閉じてしまっていたら再び呼び出し)系列のオプションマーカーグーループの中の塗りつぶしを塗りつぶしなしに変更します。
DIFFERENT VERSIONS
2010: Rに準じるならマーカーの形状 および 大きさも変更します(マーカーのオプション)
任意にその他の書式設定を重ねます。
とりわけ,
- 横・縦両軸の境界値に関する最小値および最大値の設定
- プロットエリアの縦横比の調整(正方に)
は最低限やっておいた方がbetterな項目だとは思います。
Q-Qプロットの完成です。



