2023/7/10
イントロダクション
ここでは1標本を対象とした検定を扱います。この検定では,ある比較値とある標本の平均との“差”が,統計的に意味のあるものなのかどうかを確認します。
具体的に,これは
- 帰無仮説と対立仮説を立てる
- 標本から検定統計量を求める
- 帰無仮説の下での結果の起きやすさ[確率]を求める
- 仮説を判定する
といった手順でおこないます。
以下,Excelによる母平均の検定のすすめ方です(z検定とt検定)。ここでは一連の手続きを,「Office365版」 Excel (ver.1810)で追っています。この手続きは,「永続ライセンス版」にいうところの Excel 2019, Excel 2016, Excel 2013 あるいは Excel 2010 でも変わりません。

タスクと元データ
母平均の検定について2つのタスクがあります。母集団については,ともに正規性を仮定しています。
'task A'は,リサーチサービス社の近域に本店所在地を置く会社の社長の平均年齢に関する調査,'task B'は,同じく近域で営業するラーメン店のランチセットの平均価格の調査です。
task Aは100社を,task Bは10店を,両者とも僕が無作為に抽出して調べました(標本のサイズ: 順に 100, 10)。

先輩の話によると,両タスクとも全数(とみなしていいような)調査の結果がすでに存在するようです。具体的にはtask Aの平均が58.2歳,task Bの平均が750.0円だと伝えられています。これらを比較値($\mu_0$)とします。
ただし,どちらのtaskも母標準偏差($\sigma$)は教えてもらえませんでした。したがって,ここでは母標準偏差を未知として話をすすめます。

下が両タスクについて僕が集めたデータです。今回はこれらについて統計的検定をおこなうよう先輩から指示を受けています(両側,有意水準5%。ワードについては後述)。以下,両タスクに関する検定の手続きです。

z or t?
あ。その前に
下の図は,標準正規分布の曲線(赤線)と,両タスクにおいて収集した標本のサイズ$n$にもとづく自由度$n-1$で描いた$t$分布の曲線(青線)です。どっちのタスクも母標準偏差$\sigma$が未知ですので基本的には$t$検定で問題ないと思いますが,下の図のtask Aのように,自由度にある程度の大きさがある場合には両曲線が近似することから(自由度99の図では$z$曲線と$t$曲線が重なっていて$z$曲線がわずかにしか見えません),ここではあえて標準正規分布をベースとした$z$検定を選択してみたいと思います。
またtask Bについては両曲線の近似を主張するのもさすがにちょっと無理筋な気もするので,セオリーどおり$t$分布をベースとした$t$検定をおこなうことにします。

z検定
帰無仮説と対立仮説
では,ここからtask Aの検定の手順です。
一連の流れの上では,何よりも先んじて立てられるのが帰無仮説と対立仮説です。ふつう,帰無仮説には「母集団の分布が異なることを訴えたい」とする検定の目的に鑑みて,残って欲しくない説の方を据えます。
ここでは帰無仮説として「母平均は比較値と一致している」ことを立て,対立仮説としては「母平均は比較値と一致していない」ことを立てました(両側検定)。

言い換えれば,帰無仮説は「僕のデータは平均を$\mu_0$とする母集団から抽出されたものである」ことを,対立仮説は「平均を$\mu_0$とする母集団から抽出されたものでない」ことを示しています。

あ!
ということはtask Aの場合,少なくとも帰無仮説が棄却されてしまうようでは,「どこを偏ってデータをひっぱってきたんだ!」なんて,先輩に糺されてしまいかねません,ね。標本の抽出で躓いたとなると,ウチのリサーチャーのはしくれとしてはマズいです。はたして僕の集めたデータがどうなっているのかが,とても心配になってきました。
その意味で今回は「棄却されたくない帰無仮説」という希なケースかもしれません。

検定統計量
ここから検定統計量を計算します。検定統計量は,後述の棄却限界値と突き合せたり$P$ 値を求めたりといった検定においての重要なポイントで不可欠な,いうなれば要となる値です。
さて,この標本が本当に平均$\mu_0$,標準偏差$\sigma$の母集団から抽出されたものだったとしたら(つまり,“帰無仮説は正しい” と仮定するならば),標本平均$\overline{x}$は,中心極限定理より平均$\mu_0$,標準偏差$\sigma/\sqrt{n}$(「標準誤差」)の正規分布にしたがうことが予期できます。
転じれば,標本平均$\overline{x}$を標準化したものつまり下式は$z$分布(標準正規分布)にしたがうことが明らかなので,この式を検定統計量として利用します。
あ,ええと以下,検定統計量については記号$T$であらわすことにしたいと思います。
![\[T=\frac{ \displaystyle \bar{x}-\mu_{0}}{\displaystyle \frac{\sigma}{\sqrt{n}}}\]](../images/howto/test_populationmean/step8.svg)
$T$を求めるため,必要なデータをシートに用意していきます。
まずは「(標本の)サイズ$n$」,および「比較値$\mu_0$」(ここでは全数調査の結果)です。
![[セルE2]100 [セルE3]58.2](../images/howto/test_populationmean/step9.png)
「標本平均$\overline{x}$」および (母標準偏差$\sigma$がわからないので代わりに)「標本標準偏差$s$」を求めます。前者はAverage関数 を,後者はStdev.p関数を利用します。
ただし,$n$の大きさの判断によっては不偏標準偏差(ここでは,分母が$n-1$の標準偏差を指す)の方を選択すべきだろうなと思うところではあります。$n$が大きくなれば 標本・不偏それぞれの標準偏差に大きな差が生じないのでここでは標本を使っていますが,セオリー的には例外なくStdev.s関数を充てておいた方がいろんな意味で混乱を生まないとは思います。
![[セルE5]=Average(b2:b101) [セルE6]=Stdev.p(b2:b101)](../images/howto/test_populationmean/step10.png)
「検定統計量$T$」を計算します。ここでは分子と分母に分けて計算しています。
繰り返しですが,母標準偏差$\sigma$は未知ですので標本標準偏差$s$を用います。
![[セルE9]=e5-e3 [セルE10]=e6/sqrt(e2) [セルE11]=e9/e10](../images/howto/test_populationmean/step11.png)
有意水準
あらかじめ決めておいたor指定された「有意水準$\alpha$」をタイプしておきます。これは帰無仮説を正しいとする状況下で,「めったに起きないことが起きた」と判断する“よりどころ”として使います。
今回,先輩から有意水準は5%にする旨指示されていますので,ここは0.05と入力しました。
![[セルE13]0.05](../images/howto/test_populationmean/step12.png)
両側検定
ええと有意水準を「『めったに起きないことが起きた』と判断する“よりどころ”」とひと口で片づけてしまいましたが実のところ,これには2つの考え方がありまして
ひとつは,標準正規分布の両裾あわせた任意の値(一般的には5%or1%)を判断のよりどころとするもので,この場合の検定は両側検定と呼ばれます。task Aでおこなう有意水準5%の両側検定の場合,有意水準は下の図の濃いグレーの部分の面積の和で示されます。また横軸の上・空色の太線部分は棄却域と呼ばれます。
両側検定は,ここでの対立仮説のように「差がある」ことに関心を寄せる場合などに用います。
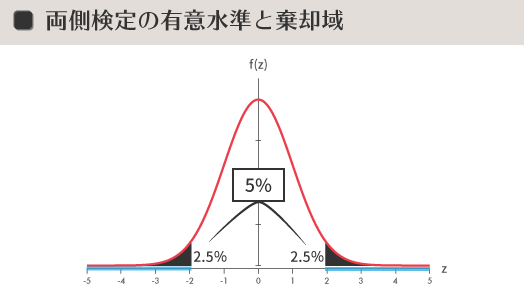
棄却限界値と棄却域
この横軸上の棄却域とその他の部分(無彩色の部分。「受容域」とも)との境界上に置かれた,2つのオレンジ色のマーカー(確率変数$z$)の指す値を棄却限界値と呼びます。先に求めた$T$が,棄却限界値を上下(図的には,「左右」とする表現のほうがハマるでしょうが)どちらかに超えてくるようであれば棄却域に入ることがわかります(帰無仮説の棄却)。
ただし 標準正規分布は左右に対称ですから,$T$の絶対値(|$T$|)をとって右側だけで判断されることも少なくありません。
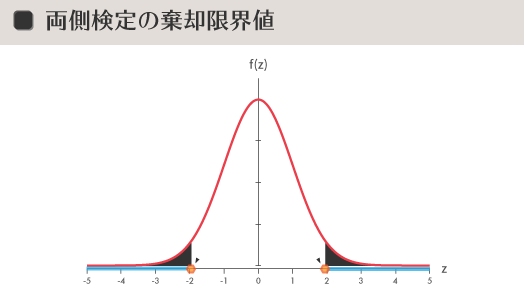
片側検定
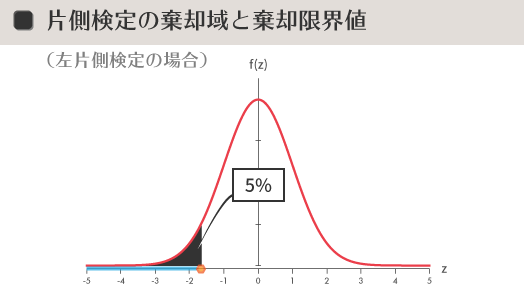
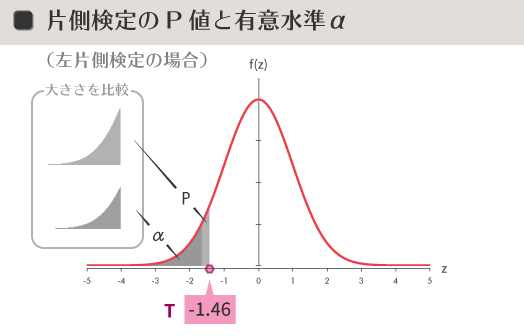
参考までに,いまひとつの判断として片側検定があります。同じ有意水準5%の片側検定の場合,有意水準(=濃いグレーの部分の面積)と棄却域(=空色の太線),そして棄却限界値(=オレンジ色のマーカー)は下の図のように示されます。
片側検定は,高い低いなど「方向性」に関心を寄せる場合などで使われます。したがって対立仮説は両側検定の場合と異なり,「$\mu_A$>$\mu_0$」あるいは「$\mu_A$<$\mu_0$」が立てられます。片側検定の場合,帰無仮説が棄却されると結果の方向性を当然のごとく決めつけてしまうことになるので,最初から母集団の間での大小関係が明白だと確信できるような場合などをのぞいては,ある意味慎重さが必要とされるかもしれません。
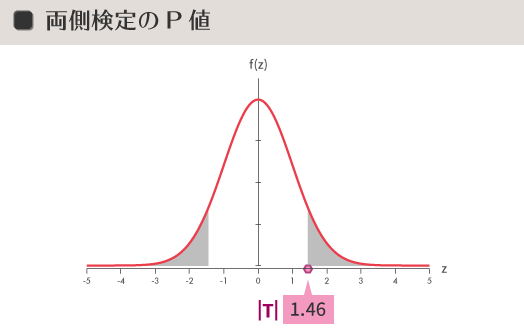
P値
それからとりわけ重要なワードとして,$P$ 値(有意確率)というものがあります。
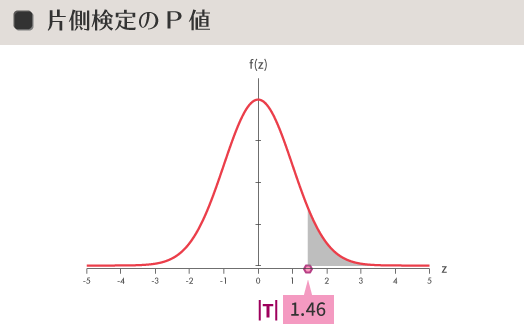
$P$ 値 とは,頁頭で据えた帰無仮説が正しいとしたときに,同じく先に求めた$T$の絶対値(|$T$|)より大きな(極端な)値が求められる確率を指して言います。言い換えれば,この標本が比較値$\mu_0$と同じ分布の母集団から抽出されたものならば,標本平均$\overline{x}$と$\mu_0$との差(1.18歳 over)は,同じ調査を繰り返したとして,いったいどの程度の頻度で発生するものなのかを示します。
両側検定・片側検定それぞれの$P$ 値を正規分布曲線に重ねると,これは下のように示すことができます。淡いグレーで彩色した部分がそれであって,正規分布曲線の下,|$T$| の外側の領域の面積が$P$ 値となります。
めったに起きないことが起きたのか?
検定の作業では,ここまでに登場した
- $T$
- 棄却限界値
- $P$ 値
- 有意水準
の各値を選択的に使って,「めったに起きないことが起きた」かどうかの判断をおこないます。とりわけ
後ろの2者,すなわち$P$ 値と有意水準の大小関係に注目すると,
- 「この差を超える標本平均となる確率は,帰無仮説の下では5%(調査20回中1回)に満たない」→「レア!」→「そもそもこの帰無仮説が正しいならこんな結果が出るのはおかしくない?」→「帰無仮説は誤りだ」(帰無仮説が棄却できる)
と判断するか,
- 「この差を超える標本平均となる確率は,帰無仮説の下で5%(調査20回中1回)を超える」→「レアでもない」→「帰無仮説が誤りだと結論付けるには無理がある」(帰無仮説は棄却できない)
と判断することになります。
以上のように,標本平均$\overline{x}$より極端な値の出る確率が,有意水準$\alpha$を超えるか超えないかを知ることが検定においてはカギとなります。この点を果たせられればよいわけですから,$P$ 値と有意水準$\alpha$のペア(以下,「方法2」)以外にも,$T$と棄却限界値の比較においても検定は可能です(以下,「方法1」)。
![何と何を照らし合わせる?[方法1]検定統計量Tと棄却限界値 [方法2]P値と有意水準](../images/howto/test_populationmean/step19.svg)
棄却限界値 or P値の計算
いずれの方法をとるにしろ,上の図の赤文字部分の値については,ここに至るまでいまだ求められてはいません。
方法1では棄却限界値が,方法2では$P$ 値がそれですが,それぞれの値は,具体的には順に有意水準$\alpha$,$T$の各値をもとに計算していくこととなります。

棄却限界値からのアプローチ
では,以上をふまえて,残る計算をしたいと思いますがええと
まずは,方法1をとった場合を示したいと思います。

方法1の場合,求めるべくは棄却限界値です(ここでは右側のそれを求めています)。片側検定の場合の値も計算していますが,task Aは両側検定なのであくまで参考としての掲示です。
- “両側”の計算式
- =NORM.S.INV(1-E13/2)
- “片側”の計算式
- =NORM.S.INV(1-E13)
標準正規分布のz(パーセント点)の求め方
![[セル16]=Norm.s.inv(1-e13/2) [セルE17]=Norm.s.inv(1-e13)](../images/howto/test_populationmean/step22.png)
棄却限界値は1.96となりました。ということで,下の図でみると$T$の値(-1.46)は棄却域(空色の太線)にかからなかったようです。
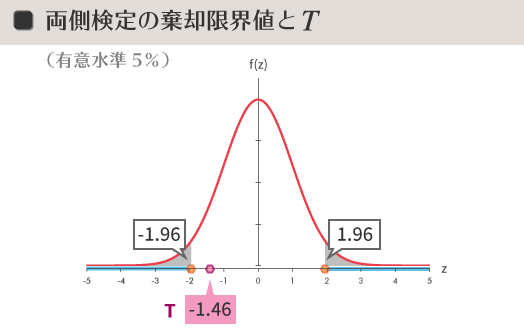
これによって「帰無仮説が誤りだと結論付けるには無理がある」こと,つまり帰無仮説が棄却できないことを示すに十分な理由ができました。したがって,この場合はさらに$P$ 値を計算しなければならない理由もありません。
ただExcelに限らず,昨今のPC環境では$P$ 値を簡単に求めることができるゆえか,僕的にはこの方法(方法1)を目にすることが少ないです。
ところでこの結果,僕的にはひとまず歓迎できるものになりました。当初の懸念が現実のものとならなくてよかったです。

P値からのアプローチ
他方,方法2をとった場合を示したいと思います。

その前に先に触れた両側検定・片側検定それぞれの$P$ 値の図を再掲しておきたいと思います。下の図で$P$ 値は,淡いグレーの領域の面積によって表現されています。


すなわち両側検定の場合の$P$ 値は,片側検定のそれの2つ分であることがわかります。ここでもそうした気づきにしたがって,前者の$P$ 値は後者のそれを2倍して求めたいと思います。
具体的には,下図のようにいったん「片側」の$P$ 値を求めて,その値を「両側」で参照するといった構造をとっていきます。もちろんセルE20のみで片側の2倍を計算してもOKです。
- “片側”の計算式
- =1-NORM.S.DIST(ABS(E11), TRUE)
標準正規分布の確率の求め方
![[セルE20]=E21*2 [セルE21]=1-Norm.s.dist(abs(e11),true)](../images/howto/test_populationmean/step27.png)
$P$ 値 は「両側」で0.14となりました。ここで$P$ 値と有意水準$\alpha$とを図示すると,下図中段のようになります(淡いグレーの部分[重複部分あり]の面積: $P$ 値, 濃いグレーの部分の面積: 有意水準$\alpha$。なお下図下段「片側」の図は参考です)。
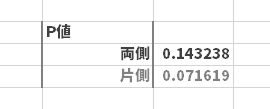
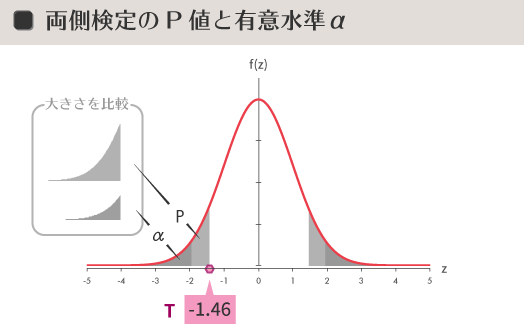
ということで,task Aの検定では $P$ 値(14%)が 有意水準$\alpha$(5%)より大きくなりました。

結局,意味のある差であったのか?
以上のとおり,方法1では
- |$T$| < 棄却限界値
となり,方法2では
- $P$ 値 > 有意水準$\alpha$
となりました。
いずれにしろこれでは帰無仮説は棄却できないので,「確率的に意味のある差ではない」と判断するしかありません(だからと言って帰無仮説そのままに「一致する」とは考えません。あくまで対立仮説を採択するには“証拠不足”であったことのみ示せます)。
また,帰無仮説が棄却された場合には対立仮説を採択します。
![[方法1]|T|<棄却限界値, [方法2]P値>有意水準α →帰無仮説H0を棄却できない:「確率的に意味のある差ではない」](../images/howto/test_populationmean/step30.svg)
t検定
ここからtask Bの検定をおこないます。基本的には$z$検定と背景は同じですので重なる説明は端折ります。
こちらも当然,まずやるべきことは帰無仮説と対立仮説を立てることです。
ということで帰無仮説としては「母平均は比較値と一致している」ことを,対立仮説としては「母平均は比較値と一致していない」ことを立てました。

母集団の正規性が仮定され,母標準偏差が未知であり,かつ標本のサイズ$n$が小さなtask Bのようなケースでは,下の標本平均$\overline{x}$に関する標準化変量が自由度$n-1$の$t$分布にしたがうことを利用して,これを検定統計量とします(以下,「$T$」)。
![\[T=\frac{ \displaystyle \bar{x}-\mu_{0}}{\displaystyle \frac{s}{\sqrt{n-1}}}\]](../images/howto/test_populationmean/step-b-2.svg)
$T$を求めるため,必要なデータをシートに用意していきます。
まずは「(標本の)サイズ$n$」と「比較値$\mu_0$」です。
![[セルE2]10 [セルE3]750](../images/howto/test_populationmean/step-b-3.png)
「標本平均$\overline{x}$ 」と「標本標準偏差$s$」を求めます。前者はAverage関数を,後者はStdev.p関数を用います。
![[セルE5]=Average(b2:b11) [セルE6]=Stdev.p(b2:b11)](../images/howto/test_populationmean/step-b-4.png)
$T$を計算します。ここでは分子と分母に分けて計算しています。
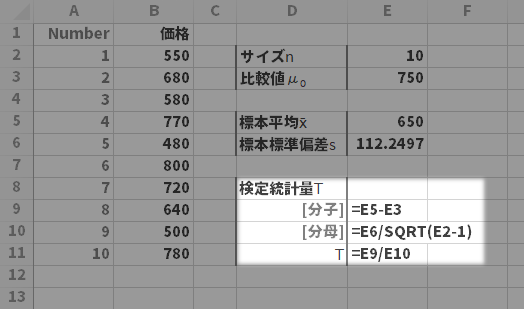
有意水準$\alpha$を設定します。
こちらも5%でおこなうよう指示されたケースですので,0.05とタイプしておきます。
![[セルE13]0.05](../images/howto/test_populationmean/step-b-6.png)
棄却限界値を求めます(これを「方法 1」と呼び,右側の棄却限界値を求めることにします)。片側検定の場合の値も計算していますが,task Bは両側検定なのであくまで参考として掲示します。
- “両側”の計算式
- =T.INV.2T(E13, E2-1)
- “片側”の計算式
- =T.INV(1-E13, E2-1)
t分布のt(パーセント点)の求め方
![[セルE16]=T.inv.2t(e13,e2-1) [セルE17]=T.inv(1-e13,e2-1)](../images/howto/test_populationmean/step-b-7.png)
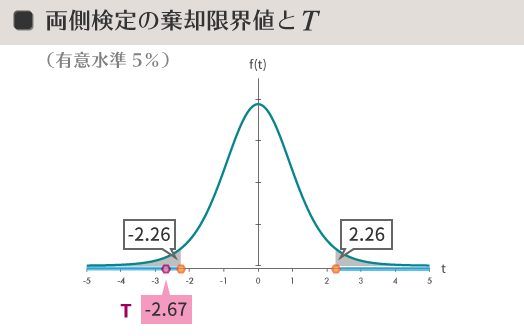
棄却限界値は2.26と返ってきました。
ということは,下の図のように$T$の値(-2.67)は棄却域(横軸・空色の太い線の部分)にかかるので,帰無仮説が棄却できます。
さて,こちらでもtask Aと同様,棄却限界値に代わり$P$ 値で手続きを進める場合(これを「方法 2」と呼ぶことにします)についても示しておこうと思います。
$P$ 値の計算式は以下のとおりです(T.DIST系の関数は両側片側で固有の関数が用意されているので,ここでも別個に計算します。もっとも$z$検定でおこなったように,両側については片側2倍でもOKです)。
- “両側”の計算式
- =T.DIST.2T(ABS(E11), E2-1)
- “片側”の計算式
- =T.DIST.RT(ABS(E11), E2-1)
t分布の確率の求め方
![[セルE20]=T.dist.2t(abs(e11),e2-1) [セルE21]=T.dist.rt(abs(e11),e2-1)](../images/howto/test_populationmean/step-b-9.png)
両側の場合,$P$ 値 は0.026となるようです(片側は参考です)。
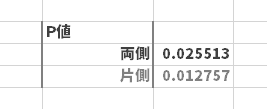
ということで,$P$ 値(2.6%)は 有意水準(5%)より小さくなりました。すなわち標本平均$\overline{x}$と比較値$\mu_0$との差(100.0円)については,「帰無仮説の下ではめったに起きないことが起きた」つまり,そもそもの仮説が間違っていたと考えます。
よって帰無仮説を棄却し,対立仮説を採択します。
にしても,こっちの結果は僕的にはマズイですけど。
![[方法1]|T|>棄却限界値, [方法2]P値<有意水準α →帰無仮説H0を棄却できる:「確率的に意味のある差であった」](../images/howto/test_populationmean/step-b-11.svg)






