2023/7/10
イントロダクション
ここでは統計的在庫管理手法のひとつ,定量発注方式を運用するのに必要な経済的発注量(EOQ)と発注点(ROP)を求めます。
一部必要な手続きに関してExcelを使っていますが,Excelでの処理はかかるテーマにおいては従としています。そのため,EOQ公式を使ってExcelでてっとり早く求めてしまいたいという場合は,以下は冗長な内容となりますのでご注意ください(出てきません)。

状況を整理する
リサーチサービス社で使用する用紙(業務用コピー用紙)の枚数です。
経理課でこれを調べたところ,1年あたり1980000枚消費していることがわかりました。したがって,単純にこれを営業日数で除してやると,1ヵ月では165000枚,1日では7500枚消費していると考えられます。
![[1年あたり消費量:1980000枚][1月あたり消費量:165000枚][1日あたり消費量:7500枚]](../images/howto/eoq_rop/step1.svg)
用紙の発注費用および保管費用です。
ここでは,前者を発注および管理事務にかかる諸費用(人件費・通信費など)および配送費用(重量にはよらないとします),後者を物的なスペースを占有することにかかる諸費用(倉庫・什器の賃借料,関連維持費など)として定義しています。とりあえず,ここでは話をひらたくして,前者は発注回数に,後者は発注量およびそれを消費することにしたがって変化する諸費用と考えておいてください。
具体的な値としては,発注費用が2000円,保管費用が1枚あたり3.216円と求められています。
![[発注費用:\2000/回][保管費用:\3.216/枚]](../images/howto/eoq_rop/step2.svg)
とりあえず,これらのデータを使って,まずは年間でかかる総費用をアバウトにシミュレーションしてみたいと思います。具体的には,
- 1年に1回だけ発注
- 1年に12回発注(つまり毎月1回)
- 1年に264回発注(これは年間営業日数に等しいとします。つまり毎日発注)
した場合の,3つのパターンを考えてみます。
あ!
話がややこしくなるとタイヘンですので,このシミュレーションの世界は,発注したら品物が瞬時に納品される世界だと,とりあえず都合のいい仮定をおかせてもらいますNe。
では,まず1年の最初に1回だけ発注するパターンを見てみたいと思います。この場合,在庫量の変化をグラフにあらわすとこんな感じになります(縦軸: 在庫量, 横軸: $t$日目)。
在庫の量は日々減っていきます。当然ながら増えることはありません。


このパターンの場合,年間の発注回数は最初の1回のみですから,発注費用は1回×2000円=2000円を要します。

年間の消費量は198万枚でしたのでこの年(とし) 1 回いちばん最初に198万枚すべてを仕入れてしまいます。
この場合,年間の保管費用は 最初に仕入れた198万枚に単位あたり保管費用を乗じた(1980000枚×3.216円)金額(6367680円)かなーとも思いましたが

先に保管費用は発注量およびそれを消費することにしたがって変化する諸費用と定義したように,よくよく考えてみれば,たとえば保管スペースなんかは常々ピーク量(最初の198万枚)と同一のキャパシティを確保しておく必要があるわけではないですね。
ピーク量を保管可能なキャパシティを維持するために必要な費用を,下のグラフに淡いグレーで重ねてみます。このとき,保管スペースのキャパシティを可変的に運用できる場合には,年間の保管費用は濃いグレーの領域であらわすことができます。これは保管費用が,キャパシティをピーク量に固定とした場合の半分となることを意味します。

上のことをふまえ,先の保管費用を再度計算すると(1980000×3.216÷2=)3183840円となります。

発注費用と保管費用をひとつにして総費用を求めます(2000+3183840)。
1年に1回だけ発注するパターンでは,在庫関連費用は3185840円必要となるようです。
![[年次一括購入の場合 在庫関連費用:\3185840]](../images/howto/eoq_rop/step10.svg)
つづいて1年に12回発注するパターンです。先に示したとおり,ひと月あたりの用紙の消費量は165000枚でしたので,毎月この枚数を月初日に1度だけ仕入れていきます。

在庫量の変化をグラフにすると,こちらはこんな感じですね(下図)。
先とは異なり,グラフは櫛型となりました。

月ごとに発注をかけますので,山の数は12です。
また先と同様,年間の保管費用は淡いグレーの部分の½となることがわかります。

この点をふまえ,次の式で具体的に発注費用と保管費用を計算してみます。

えーと1年に12回発注するパターンでは,在庫関連費用は289320円必要となるようです。
![[月次一括購入の場合 在庫関連費用:\289320]](../images/howto/eoq_rop/step15.svg)
今度はこれまた極端ですが1年に264回発注するパターンです。毎日の業務に必要な7500枚を日々仕入れていきます。

在庫量の変化のグラフはここんなふうになりました(下図)。
レイアウトの制約上 系列線で潰れていますが拡大するとこちらも櫛型の山があるんです。


毎日発注をかけますから,山の数は264(=年間営業日数)です。
またこれも以前の2つのパターンと同様,年間の保管費用は淡いグレーの部分の½となります。

この点をふまえ,同じように次式で具体的に発注費用と保管費用を計算してみると

在庫関連費用は540060円必要となることが示されました。
![[日次購入の場合 在庫関連費用:\540060]](../images/howto/eoq_rop/step20.svg)
以上の3パターンの結果を,下にあらためて提示します。
最初に掲げたリサーチサービス社のデータ(設定)のもとで,在庫に関する総費用を考えるとき,こんなことが言えそうです。
- 1年分を一括で仕入れるより,1ヵ月分を一括で仕入れた方が おトク
- 1ヵ月分一括仕入から,毎日の仕入れに切り替えると かえって損

経済的発注量を求める
そういったコトが明らかになってくると,少し欲が出てきました。
というのも,上に見た3つのパターンはあくまで便宜上の区分にすぎないです。ひと月1回,1ヵ月の必要量である165000枚を発注していけば年間の在庫関連費用を最も小さくできるという最適解を示すものではありません。以後,この点を考えていきたいと思います。
その前に定量発注方式では,その名のとおり最適な発注量を定数(≒変化させない)として考えます。ここで,その定数 すなわち1回あたりの発注量を$x$と定義しておきます。

ではまず
先の3つのパターンから,年間に要する発注費用の計算式を一般化してみると
- 年間発注費用=年間の発注回数×1回あたりの発注費用
であらわすことができます。

ここで,(1回あたりの発注量を$x$としたので)年間の発注回数は
- 年間消費量$÷x$
であらわすことができます。「年間消費量」については具体的な値がわかっていますので(設定),これを代入し
- $1980000÷x$
とあらわせます。

この式,および1回あたりの発注費用(設定)を
- 年間発注費用=年間の発注回数×1回あたりの発注費用
式に代入すると,
- 年間発注費用$=3960000000÷x$
とすることができます。

年間発注費用=3960000000÷$x$ 式をグラフに描画してみると,下図のようになります(縦軸: 年間発注費, 横軸: $x$)。

つづいて同じように
先の3つのパターンから,年間に要する保管費用の計算式を一般化してみると
- 年間保管費用=1回あたりの発注費用×1単位あたりの年間保管費用÷2
であらわすことができます。

「1単位あたりの年間保管費用」については具体的な値がわかっていますので(設定),これを代入し
- $x×3.216÷2$
とあらわせます。

すなわち年間保管費用は
- 年間保管費用$=1.608x$
となります。

年間保管費用=1.608$x$ 式をグラフに描画してみると,下図のようになります(縦軸:年間保管費用, 横軸:$x$)。

これを先ほどの年間発注費用のグラフと重ねてみると下のようなグラフとなりました。

ここで,在庫関連費用は総費用(発注費用+保管費用)ですから,
- 年間在庫関連費用$=3960000000÷x+1.608x$
とあらわすことができます。

この年間在庫関連費用=3960000000÷$x$+1.608$x$ 式を先のグラフに重ねます。下図オレンジ色の線がそれです。

年間在庫関連費用が最も小さくなるのは,オレンジ色の線上に置いた青色の点の位置となることがわかります。つまり,このときの横軸上の赤色の点が,年間在庫関連費用を最も小さくできる$x$(1回あたりの発注量)となるはずです。

この$x$の具体的な値を知るために,下図緑色の点に注目します。
“「発注費用」線と「保管費用」線の交点で,年間在庫関連費用が最も小さくなっている”ということを利用すると

発注費用=保管費用 となる式
- $3960000000÷x=1.608x$
を導くことができます。これを任意の手段で$x$について解けば具体的な値が求められます。

参考ですが次のように式を整えて,便利なWebサービス「Keisan-高精度計算サイト」で求めてしまうのが手っ取り早いかもしれません。
いずれにしろ,結果は $x=49625$ となります(マイナスの発注量は現実的でないのでプラスの方のみ解とします)。

リサーチサービス社の環境のもとでは,都度49625枚発注していくと年間在庫関連費用を最も小さくできることがわかりました。
なお,ここで求めた値は経済的発注量(EOQ)と呼ばれます。

![[セルA4]EOQ [セルB4]49625](../images/howto/eoq_rop/step38-2@1x.png)
発注点とリードタイム
最初の設定に却って1日あたりの消費量が7500枚でしたから,このEOQは6.6日分の消費量に相当することとなります。

と,いうことで下図の上段のパターンすなわち49625枚発注・入荷して,6.6日後に在庫がなくなるはずなのでそのときまた49625枚発注・入荷してというパターンで運用のプランが立ちそうですが実際の現場では,こんなに都合よくコトが運ぶはずもないんです。
ここまで発注と入荷の時間差の存在しない世界を仮定してきましたが,第1の課題として,実際にはリードタイム(ここでは発注後入荷までの所要日数とします)が存在します。となれば,下段のように在庫が底をついてからあらたな用紙が入荷されるまで(淡いあずき色で彩色した期間),ウチの場合は業務が止まってしまうことになります。

したがって,リードタイムが存在することを鑑みて,発注のタイミングををいくらか先取りしていく必要が生じます。
この「いくらか」を具体的に示すものとして,定量発注方式では 発注点(ROP: ReOrder Point)と呼ばれる物量的なタイミングを設定します。ここから後の説明は,この発注点を求めていく過程となります。

ということで,リードタイムが情報として必要です。
現在の業者さんとの取引で,このリードタイムは3日となっています。
![[リードタイム:3日]](../images/howto/eoq_rop/step42-1.svg)
![[セルA6]リードタイム [セルB6]3](../images/howto/eoq_rop/step42-2@1x.png)
用紙を発注して納入されるまでに3日を要しますから,この期間中消費される予定量 すなわち22500枚をあらかじめ見込んで発注のタイミングをはかります。具体的に,在庫残数が22500枚に到達した時点で発注をおこなえば業務を止めることなくスムーズにサイクルをまわせそうに思えます

「安全在庫」も加味してみる
が。やっぱり,何かが足りないですね。
ここまで何の気なしに「1日あたり消費量」というワードを使ってきましたが,現実にはこれは定数ではありません。年間のスパンで考えた場合,リサーチサービス社では,1日あたり平均7500枚消費することに誤りはないのですが,日々の消費量には若干の多寡が生じています。
![[1日あたり平均消費量:7500枚]](../images/howto/eoq_rop/step44-1.svg)
![[セルA1]1日あたり平均消費量 [セルB1]7500](../images/howto/eoq_rop/step44-2@1x.png)
となれば下図上段のように入荷・発注・在庫切れのサイクルが6.6日のスパンで規則正しく繰り返されることはまずありません。
場合によっては,下段のようなパターンになるかもしれません。たとえば最初は入荷から発注までが3.6日,そこから在庫切れ(つまり再入荷)に至るまでが3日(=リードタイム)という流れであったものが,次のフェーズではより速いペースで消費され(図の 水色の角度>赤の角度),発注点までより早く到達する(2.6日)そんなケースです。
このパターンのように,定量発注方式では入荷から発注点までの日数は消費のペースにしたがって変化します。

何より問題なのは,発注点以降の消費量です。
すでにリードタイム中の消費量として22500枚という値を導いていますが,先の話から,こちらも平均たることを考慮していかなくてはならなくなります。
後出しの情報になりますが,今回,毎日の消費量は正規分布にしたがっていることをあらかじめ見越しています。これを前提として,下にリードタイム中の消費量の正規分布曲線を描いてみます。下図の淡い茶色の領域で示されるように,リードタイム中(=3日間)の消費量は50%の確率で22500枚を超えてしまうことがわかります。

換言すると
発注点後(=発注してから入荷されるまでの間),今の計画のままでは在庫を切らしてしまう事態が2回に1回 は起こってしまうワケです。
第2の課題として,これを何とかする必要がありますね。結局,このままでは業務への影響が大きいですし。

と,いうことで第2の課題を解決するために,黒い線をつまんでリードタイム中欠品が生じないような高さまでぐぐぐーっと引っ張り上げてやります(下図)。
こうしていくらかのゲタを履かせてしまえば,リードタイム中に在庫が切れる確率を50%より減らすことができます。この線を引っ張り上げたことによって現れた紫色部分の高さ(=用紙の枚数)は安全在庫と呼ばれます(下図)。

こうして安全在庫を加味する場合,発注点にもそれを反映させてやる必要がありますね。したがって,リードタイム中の消費量(22500枚)に安全在庫を加えた値をあたらしい発注点として再定義したいと思います。

と,なれば 業務が止まるのは私(わたし)的にもまずいですし,やっぱりこの安全在庫はすっごくたくさんの量を確保しといたほうがいいのかも
と,一瞬考えてしまいましたが それも本末転倒,ですね。
私はそもそも,在庫関連費用を可能な限り抑えようとこの問題に取り組んでいるはずでした。在庫切れを極度に恐れるあまり,在庫関連費用の問題を無視してしまうのでは意味をなしません。
ということで,ここに「安全在庫をどの程度に設定すべきか」というあらたな課題が生じます。

さて,先ほどリードタイム中の消費量に関して正規分布曲線を描画しました。と,いうことはこちらも後出しの情報となって申し訳ないのですが,1日あたりの消費量についての標準偏差もあらかじめ見当をつけています(1650枚)。
![[1日の消費量の標準偏差:1650枚]](../images/howto/eoq_rop/step52-1.svg)
![[セルA2]1日あたりの消費量の標準偏差 [セルB2]1650](../images/howto/eoq_rop/step52-2@1x.png)
リードタイムは3日ですから,先ほどの正規分布曲線は3日分の標準偏差で描いています。ここで説明の都合上,一時的に リードタイムを$t$日とし,1日の消費量の標準偏差を$\sigma$とします。
まとまった日々の観測値が存在するなら,$t$日分の移動合計をとって標準偏差を求めるか,あるいは$t$日分の標準偏差は おおむね
- $\sigma\times\sqrt{t}$
と近似することを利用して,リードタイム日数分の消費量の標準偏差を計算します。なお,このあたりのロジックについては私なんかよりこちらの解説に明るいです。
とまれ,後者の方法で求めると2858枚($1650\times\sqrt{3}$枚) となります。先ほどの正規分布曲線を描画するのに必要な標準偏差は,この値を用いています。

![[セルA8]リードタイム期間中の標準偏差 [セルB8]=B2*SQRT(B6)](../images/howto/eoq_rop/step53-2@1x.png)
1日の消費量が正規分布にしたがうという前提のもとでは,在庫切れの可能性を確率的に限りなく低くすることはできても,結局,完全に排除することはできません。したがって「安全在庫をどの程度に設定すべきか」については,緊急的な在庫切れに際しての対応策を用意した上で「どの程度の頻度までなら在庫切れを許容できるか」の方を考えた方がこころ持ち的にもよさ気です。
実際の運用経験のない私にとっては悩ましいところですが,ま初めてですしここでは20回に1回くらいの確率を許容することで様子を見てみようかなと思います(危険率: $5/100=0.05$)。

![[セルA10]危険率α [セルB10]0.05](../images/howto/eoq_rop/step54-2@1x.png)
ということで20回に1回の確率で在庫が切れるケースを考えてみます。
下図 リードタイム中の消費量に関する正規分布のグラフにおいて,右から5%の領域を占める用紙の枚数はポインターの先端で示されます(上側5%点)。Excelでパーセント点を求める関数は累積(下側)確率を引数に求めてきますので,ポインターの先端の具体的な値(パーセント点)は下図の淡い茶色の領域の面積(95%)を使って計算することとします。

では,具体的に 上側5%点を計算してみます。
下の図のようなシートの構成のとき,
- =NORM.INV(1-B10, B7, B8)
という式で求められます。
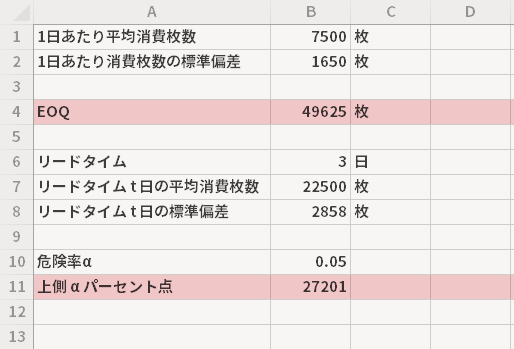
![[セルA11]上側αパーセント点 [セルB11]=NORM.INV(1-B10,B7,B8)](../images/howto/eoq_rop/step56-2@1x.png)
上側5%点つまりあたらしい発注点は27201枚 となりました(27201-22500=4701枚が安全在庫であることを意味します)。
結果,以上の手順で導いた定量発注方式による発注プランとして,
| 発注量 | 49625 枚 |
| 発注点 | 27201 枚 |
とする案が用意できました(完了)。