2023/7/10
イントロダクション
「ナイーブ(naïve)な予測」とは,次の1期の定量的な予測値を用意する必要に迫られたとき,直前の実測値をそのままスライドさせて“予測値”に充てる方法を指します。ここで扱う方法はその単純さを踏襲しつつも,「そのまま」ではなく指数平滑移動平均を使います。
READ MORE
念のため,ここにいう「ナイーブ」は,英語圏でいうネガティブなニュアンスを保持したものです。予測という行動にシャープな論理性を同伴させる目的では薄弱ですが,裏を返せば取っ掛かり易いシンプルなルールであるので,ユーザーが他にノウハウを所持していなければ,もっとも利用しやすい部類の方法と言えます。
ただ,ナイーブなアプローチをとるにしろ,いかんせんここで扱う売上のようなデータは,変動要素(スパンによっては季節変動, あるいは無作為な変動)を含むのが常であって,ときに許容しがたい誤差を抱えることがあります。単純な方法をとる以上「それも止む無し」と言えばそれまでですが,どうせならそうした変動の影響力を少しでも弱められるにこしたことはありません。この手段として,「指数平滑移動平均」をとる平滑化のプロセスを介在させます。
前頁で見た移動平均法との差異は,
- 移動平均法:先行する各期の実測値は,扱いの上で対等(たとえば,6ヵ月の売上の移動平均をとるなら,先行する6ヵ月の各月のデータは同じ重要さを持つと考える)
- 指数平滑法:同,扱いの上で直近のデータほど重きを置かれる(過去に向かって重要さは指数関数的に減少:文中で触れます)
に際立ちます。
さらに移動平均法に対して指数平滑法の長所は,
- より少ないサイズ(データの数)でも予測というアクションを起こすことができる
ことに尽きるかと思います。
また,ここでの例のように,最初の予測値=1期目の実測値 として処理を進めた場合,
- 計算に利用する観測値のmax.を超える,あるいはmin.を下回る値を予測値として出すことはできない
といった移動平均法の場合と同様の制限を含みます。
以下,Excelによる指数平滑法を使ったナイーブな予測の流れです。ここでは一連の手続きを Excel 2016 で追っています。一部ボタンの配置や名称などが異なる箇所がありますが(この場合,可能であれば当該箇所に明記します),手続きそのものは,「永続ライセンス版」にいうところの Excel 2019, Excel 2013 あるいは Excel 2010,そして,「Office365版」の Excel (本頁更新時点のver.1905)でも基本的には同じです。

元データ
元のデータです。ある販売担当部員のここ1年の売上を月ごとに集計したものです。
左の「期」列はデータの数を分かりやすくするため便宜的に挿入したものです。ですので処理上,なくてはならないもの!というわけではありません。
このデータより13期目(9月)の売上の予測値をつくるのが目的です。
なお,すぐに項目を追加するので,表の上部に1行分の空白行を残しておいた方がbetterです。
αを9個のパターンで考える
あたらしく見出しを作り,値を入力します。
下のようにα(アルファ)および0.1を入力し(ここでは順に セルD1, E1),その下の行に見出し予測値と絶対誤差(ここでは順に セルD2, E2)を作ります。
すべて終えたら,これらを右に1ブロック分(2列)だけコピーします。
![[セルD1]α, [セルE1]0.1, [セルD2]予測値, [セルE2]絶対誤差。セル範囲D1:E2を右に1ブロック分コピー](../images/howto/f_exsmooth/step2.png)
あたらしくコピーされた方のブロックについて,値部分を修正します。
具体的には,下のように前のブロックのαの値に0.1だけ加える式に書き換えます。
- =E1+0.1
![[セルG1]=E1+0.1](../images/howto/f_exsmooth/step3.png)
αの値が0.2のブロックを選択し(4つのセル),これをαの値として0.9となるブロックができるまで(残り7ブロック分)右方にコピーします。
この例では,U列までのコピーによってすべてのブロックを用意することができます。

予測式にあてはめてみる
では以降,各々のブロックごとに予測値と絶対誤差を計算していきます。
まずは次の期の予測値についてですがこれは下の上段の式で計算します。
ただ,ことばでこれを示すのも以下冗長かとも思いますので,ここではFtをt期の予測値,Xtをt期の実測値として,下の下段のような表現を使いたいと思います。

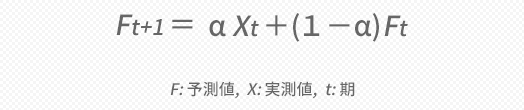
「α」は平滑(化)定数と呼ばれ,ある意味,この手法のキモとなる要素で“重み(以下「ウエイト」)”の役割を担います。
またこのαは,0<α<1の範囲をとります。そこで先にα=0.1~0.9まで総当たりで計算するため,9つのブロックを作っておいたというわけです。
指数平滑法を扱う以上,このウエイトの部分をスルーして手続きを追っても,発表などで数字の背景について説明を求められたとき,あわあわしてしまうのが関の山なので,以降,適宜この話に触れていきたいと思います。
というわけで,ここでもαについてちらっと眺めておきたいのですが,直前のstepで掲げた式ではαが2か所差しこまれているのがわかります。前段がXtに掛かるα,後段がFtに掛かる(1-α)です。
つまり片方に掛かるウエイトが増えれば,もう片方のそれが減るといった関係にあることがわかります。
仮に先のルールを曲げるとして,αが境界の値をとることができたとして話を進めると,Xtのαに全振りした場合(α=1)には,
(次の)予測値=(直前の)実測値
となり真の意味でのナイーブな方法と変わりません。反対にFtに全振りした場合(α=0)には,
(次の)予測値=(直前の)予測値
といったこちらも(意味があるかどうかは別として)ごく単純な予測のアルゴリズムとなることがわかります。
すなわちウエイトαの値の大小は,当期の実測値に重きを置いて予測をするのか,それとも(当期の「実測値」に対応する)予測値にそれを置いて予測をするのかを決定づけます。

では具体的な手続きに戻ります。
とはいえ,5式で,予測には先の期の予測値が必要とされました。ここで1期目は予測値が存在せず,ゆえに2期目の予測ができないことがわかります。したがって新規で予測をつくる場合はこうした初期値の設定がいくつかの方法で必要となりますが,この例では,2期目の予測値にはそのまま1期目の実測値を参照する,ごく単純な方法をとっていきます。
なお,後にコピーすることを考慮して,これは絶対参照としておきます。
- =$C$3
![[セルD4]=$C$3](../images/howto/f_exsmooth/step7.png)
これ以降は5式をそのまま利用することができます。
具体的に,α=0.1のときの3期目の式は,
- =E$1*$C4+(1-E$1)*D4
となります。こちらもコピーすることを考慮して,C4のセルとE1のセルについては複合参照にしておきます。
実測値の“列”とαの値の“行”についてのみ固定。
入力できたら,この式を表の最下行より1つはみ出るところまでコピーします。
![[セルD5]=($C4-D4)*E$1+D4。この式をセルD15までコピー](../images/howto/f_exsmooth/step8.png)
一旦手続きをお休みして上での作業を振り返ってみます。
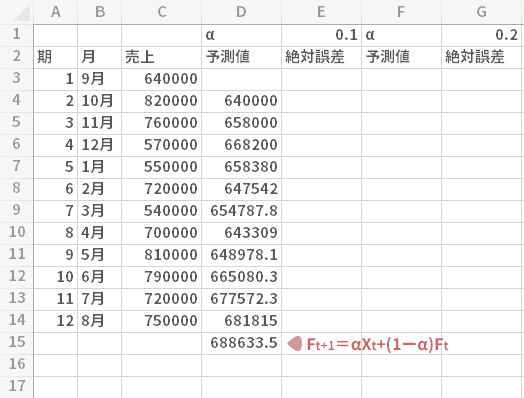
時間の流れの中でもっともあたらしい期,すなわち第12期をtとしたとき,次の期の予測値Ft+1は5式に則って,t期の実測値,および予測値にそれぞれウエイトを乗せて下の上段の図のように求めました。
t期以前の予測値についてもこの構成は同じであって,これらをすべて示せば下の下段の図のようにあらわすことができます。
ただし第2期のみ第1期のXを流用。
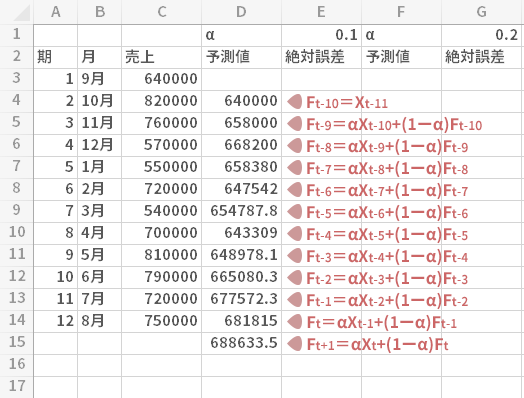
こうして細かに見ていくと,下のように緑色で彩色した,連綿とした流れがあることに気づきます。
すなわち過去におこなった予測について,程度の差こそあれ(後述)すべての結果を取り込むかたちでFt+1の計算がおこなわれていることがわかります。
またXについてはどうかといえば,直前の期のそれのみが参照される構造のようです。したがって,移動平均法とは対照的に,ある程度のサイズのXを揃えられなくても計算そのものは可能であることがわかります。
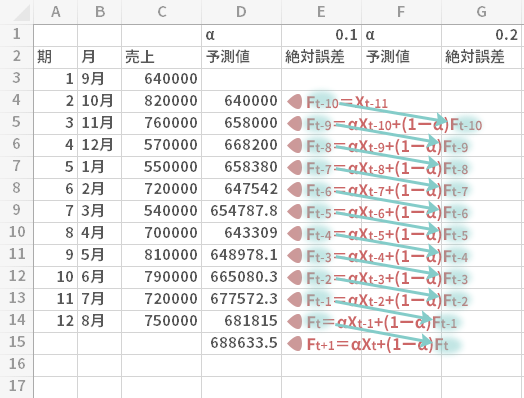
上でお話ししたいくつかのことより,おのずから次のことが見えてきます。
- αが0に近づくほど,過去からおこなってきた一連の予測,すなわち「連綿とした流れ」にウエイトを置く。
- 反対にαが1に近づくほど「連綿とした流れ」に向かう関心は相対的に軽くなり,転じて当期の実測値,つまり変化に対する敏感さ,ワードを換えれば「フットワークの良さ」にウエイトを置く。
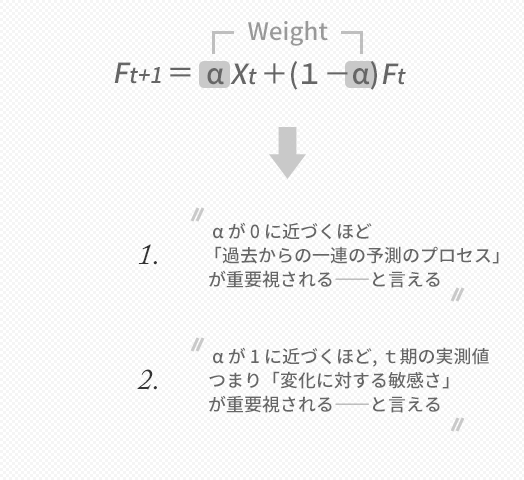
上の2.について,当期の実測値を重要視することがなぜフットワークの良さにつながるのか,ここはいまいち理解のしがたい部分かもしれません。
そこで,5式を再掲します。
- Ft+1=αXt+(1-α)Ft
この式をαでくくりなおして変形してやると,次の式を導くことができます。
- Ft+1=α(Xt-Ft)+Ft
下の図にいうこの式の強調部分はXt-Ft,すなわち誤差に相当する部分です。この誤差にウエイトαを掛け,それを先期のFに加算して予測値をつくっていることがこの式では示されますが,ここでαが大きいほど,次の予測に誤差をそのまま組み込んで修正していくかたちになることがイメージできます。「フットワークの良さ」については,こうしたことを言っています。
ただし念のため,“フットワークが良い=すぐれた予測”になるわけでも,“連綿とした流れを大切にする=すぐれた予測”になるわけでもありません。この点については強調しておきたいと思います。
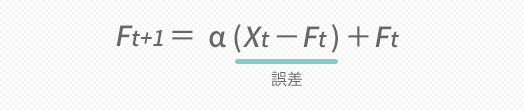
さて次に,10ではことばで掲げたにすぎなかった「連綿とした流れ」を,あらためて数式によってあらわしてみたいと思います。
まずは表の最下行,次期予測のFt+1は,10図からもわかるとおり
- Ft+1=αXt+(1-α)Ft
でした。ここで末尾のFtは,同じように10図から
- Ft=αXt-1+(1-α)Ft-1
であったので,これをそのまま最初の式に突っ込んでやると,下の上段の式が導けます。
これと同じことを,時間を戻すように1つずつ延々と遡ってつづけていくと,下の下段のような結果となります。
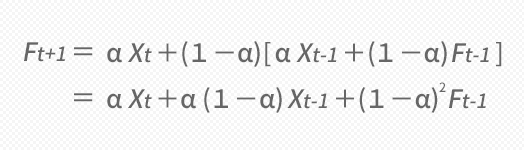
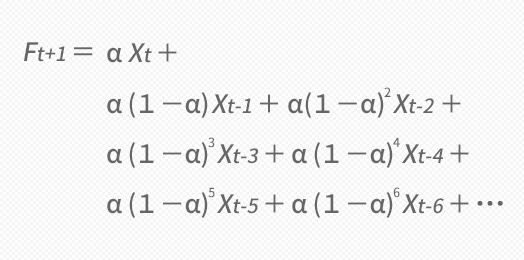
次期の予測値は,実のところウエイトが掛けられた当期から過去の各期の実測値Xを合成したものであることを見てとれます。
ここで再び注目したいのが,まさにその「ウエイト」です。
下の上段の図,緑で彩色して示した箇所のように,掛かってくるウエイトが各期のXでそれぞれ同じでないことに気づかされます。
ということでたとえばの話としてαに0.5を投げてみたいのですがとりあえず,これについてウエイトα(1-α),α(1-α)2だけを求めてみると,下の下段の図のような値が返ってきます。
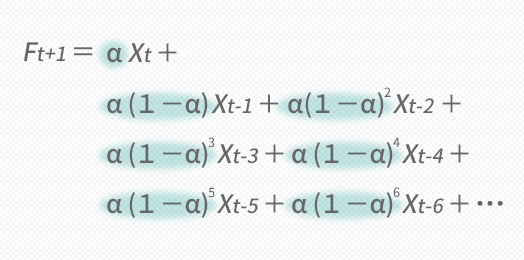
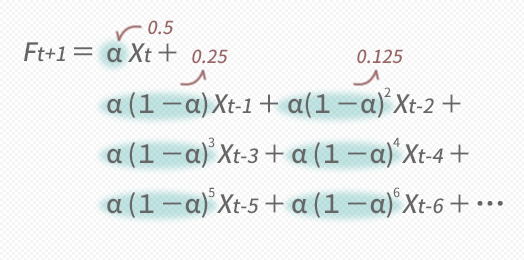
こうしてXに掛かるすべてのウエイトを求め,グラフにプロットしていくと下のような図が出来上がります。
- ウエイトは,過去に向かって指数関数的に減少していく。
まさにこの特徴が「指数」平滑法という呼称の由来となっています。このように,指数平滑法ではより近くのXから相対的に重要とされる扱いを受けていきます。
誤差を計算しておく
これ以降,具体的な作業に戻ります。
ここでは,絶対誤差を求めます。式は
(実測値-予測値)の絶対値
です。具体的には
- =ABS($C4-D4)
と入力します。ここでも,実測値「売上」の“列”(ここではC列)については,コピーすることを想定して固定しておきます(複合参照)。
入力できたら,この式を表の最下行までコピーします。
![誤差の計算…[セルE4]=ABS($C4-D4)。この式をセルE14までコピー](../images/howto/f_exsmooth/step16.png)
先ほど計算式を入力した領域を選択し(下の図のハイライトの部分),αの値が0.9となるブロック(このケースではU列)まで一気にコピーします。

予測値として採用する値を絞り込む
予測ですから13期,ここでいう9月の行見出しを下のように用意しておきます。
すなわち青の着色部分(計9個。下の図は一部のみ)の値が次期の予測値(この時点では候補)ということになります。
![[セルA15]13, [セルB15]9月](../images/howto/f_exsmooth/step18.png)
ここより,αの値の分だけ計算した9個の予測値のなかから,よりフィットしそうだと思われる値を絞り込んでいくためのしくみを整えていきます。
その第一として,下のような見出しと値を入力しておきます(3ヵ所)。
なお,ここでいう「区間」とは,絶対誤差の平均を求める際に,対象として組み入れる期数のことを指しています。ここでは,とりあえずの数字として「3」と入力しておきました。
![[セルA17]区間, [セルB17]3, [セルD17]誤差の平均](../images/howto/f_exsmooth/step19.png)
第二に,α=0.1のときの誤差の平均を計算します。
見出し「誤差の平均」のすぐ右のセル(ここではセルE17)に,次の計算式を入力します。
- =AVERAGE(OFFSET(E14, 0, 0, $B$17*-1, 1))
この構造の式は別頁「移動平均法による単純予測 with Excel」でも使用しています。関数の役割など仔細についてはそちらで触れていますので,必要があればリンク先にて確認ください。
![平均誤差の計算…[セルE17]=AVERAGE(OFFSET(E14,0,0,$B$17*-1,1))](../images/howto/f_exsmooth/step20.png)
上で入力した計算式とその1つ右の空白セルを選択し,αの値が0.9となるブロック(この例ではU列)までコピーします。
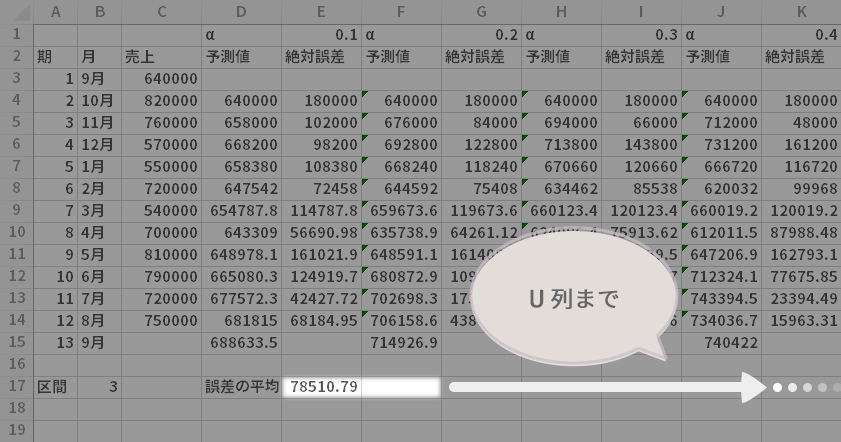
指数平滑法による次期の予測,および各平滑定数(α=0.1~0.9)を採用した場合の誤差の平均について計算ができました。
表としては以上で完成です。
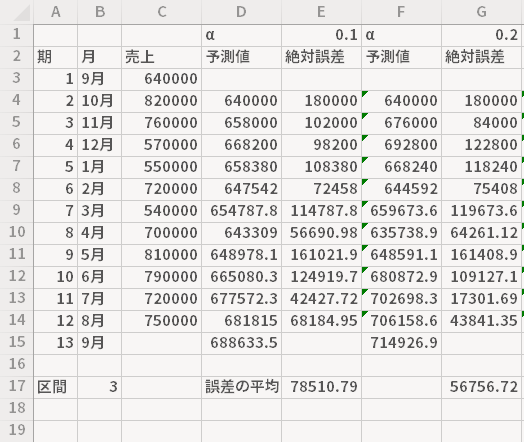
ここから少しTipsを加えます。
シートの「区間」の値を変更する都度,誤差の平均について再計算がおこなわれます。式の修正を必要としないので,適当と思われる区間を推量していく際に,いろいろと数字を変えてサクサクと検討できるかと思います。
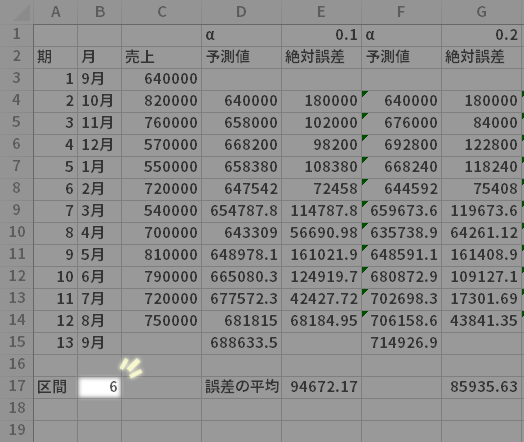
たとえば,直近の6期(区間6)における誤差のみを考慮に入れたい(重要視したい)場合,もっとも小さな平均は,α=0.3のブロックにあるそれであることがわかります(青色の着色部分)。このα=0.3としたときの13期目の値(緑色の着色部分)を,次期の予測値として採用するといったことが可能です。
いつまで遡って誤差を考慮に入れるかつまり期数については一概に言えるものではないですが,移動平均法と違い そもそもいくらか前のXのもつ影響力はほぼ無視できる程度になるので,そうした点を鑑みれば必ずしもすべての期間でとらなければならない理由もないと考えます。この例のように11期分の誤差を求めた場合,現実的なその判断の場面では半数程度も加味すれば十分でしょう。もちろん,判断に迷えばすべての期を取り入れて計ってやってもよいかと思います。
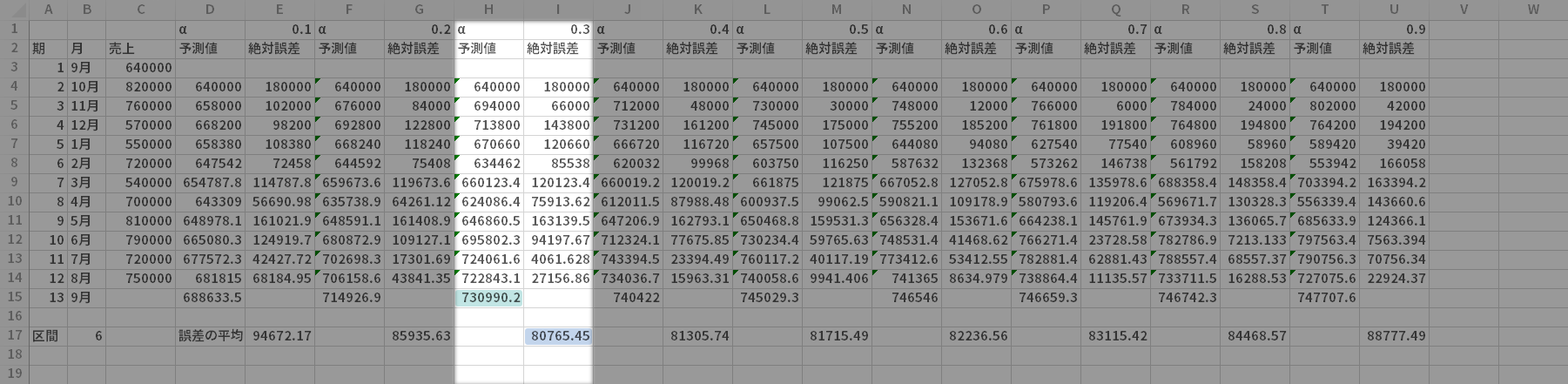
あわせてグラフを作る場合
それからグラフが必要な場合にはB, Cの2列と目的のαの「予測値」列とを選択して,移動平均法と同様折れ線グラフで描画します。
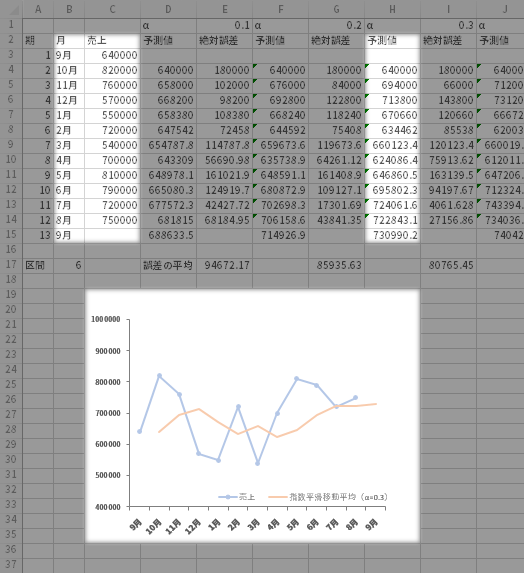
参考までに,上の手続きプラスアルファで,たとえば次のようなグラフを作ってみました。
実測値(実線)に対して異なるαによる予測値を並べています(破線)。この頁の中盤あたりで見たとおり,αの値が小さな方がより大きなそれよりも,さらに平滑化されていることを窺うことができます(「連綿とした流れ」に重きが置かれる)。
ソルバーによるαへのアプローチ
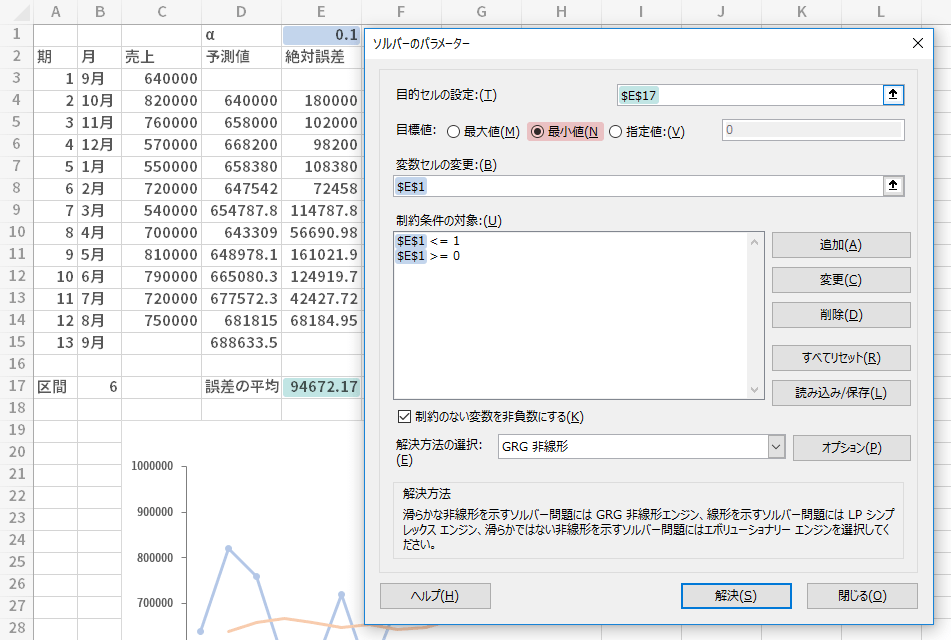
最後に,αの求め方についてはソルバーを利用する方法もあります。
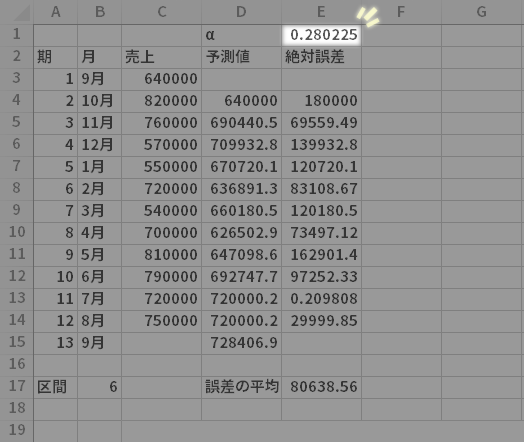
具体的には下の上段の図のような設定で,誤差が最小となるαの値を0<α<1という制約の中からソルバー機能によって探索させ(ただしソルバーの仕様に縛られるので,下図では「両端を含まない」制約を曲げています),このページでの作例で導いたαよりさらに精緻なαの値を,下の下段の図のように求めることができます。
この場合,予測値と誤差の列は1ブロックだけ用意すればいいといった点では効率的です。ただアドインが導入できるor稼働している環境であることが前提となりますし,複数のアウトプットが必要な場合や区間を変化させた場合には都度ソルバーを走らせる必要に迫られるので,シートの再計算に係る利便性を大事にしたい場合には,適用が難しいかもしれません。