2023/7/10
イントロダクション
相関分析のツール,散布図・相関係数を描画・計算します。変数どうし,互いの関係をビジュアルに表現するのが散布図で,定量的に表現するのが相関係数です。
READ MORE
相関係数($r$)は$-1$から$1$の範囲の値をとります。このとき,$-1\leqq r<0$の範囲を負の相関,$r=0$のものを無相関,$0<r\leqq 1$の範囲を正の相関と呼びます。
相関は,$r$が負であれば$-1$,正であれば $1$ に近づくほど強く,反対に $0$ に近づくほど弱いと判断します。このような相関の強弱について,相関分析に触れた書籍などでは,概して数段の階層的判断基準が併載されているのを見かけます。そういった絶対的な基準は目安としてユーザーの判断をたすけてくれますが,そもそも相関係数が順序尺度である以上,ユーザーの経験に照らして比較するなど時として相対的な見方をもって判断を補うことが望まれる場面もないわけではありません。
以下,Excelによる散布図の描き方と相関係数の求め方です。ここでは一連の手続きを 「Office365版」の Excel (ver.1908) で追っています。一部ボタンの配置や名称などが異なる箇所がありますが(この場合,可能であれば当該箇所に明記します),手続きそのものは,「永続ライセンス版」にいうところの Excel 2019, Excel 2016,Excel 2013,あるいは Excel 2010 とも基本的には同じです。

元データ
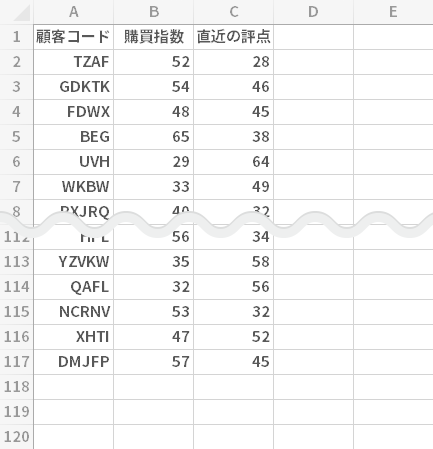
元のデータです。
顧客マスタに存在する,ある業種の顧客すべてについて,購買指数(ここでは,売上金額と販売回数の各実績値をもとに算出した値を意味します)と直近の評点(ここでは,企業活動に係る総合スコアのようなものと考えてください)を抽出したものです。
このデータから,相関分析に必要な散布図を作成し,相関係数を求めます。
散布図からデータを眺める
大きな流れの第一として,散布図を作成してデータの概観から捕捉していきたいと思います。
「購買指数」列と「直近の評点」列のデータを見出しを除きすべて選択します。
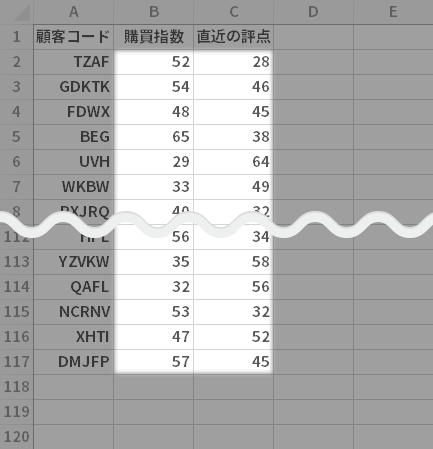
リボンの挿入タブグラフグールプにある散布図(X, Y)またはバブルチャートの挿入ボタンをクリックします1。
つづいて プルダウンメニューから散布図ボタンをクリックします2。
DIFFERENT VERSIONS
1 2010: 挿入タブグラフグールプにある散布図ボタン
2 2010: 散布図(マーカーのみ)ボタン
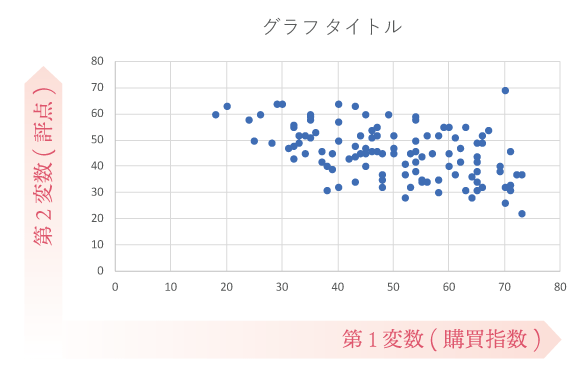
プレーンな散布図が出来ました。このとき,グラフの横軸がシートのB列の値(第1変数:「購買指数」列のデータ),縦軸がシートのC列の値(第2変数:「直近の評点」列のデータ)です。
2つの変数… どっちが横でどっちが縦?
第1・第2変数をそれぞれ横縦どちらの軸に置くべきかについては,ここでのような「相関分析」の範囲に限れば,自由に決めればOKです。Excelの仕様としては,シートの上で最も左方に存在する変数(ここでは「購買指数」)が横軸に振られます。
ただ,ここでは扱いませんが2つの変数の関係にはっきりとした方向性をおく「回帰分析」につなげることが視野にある場合には,説明変数とする方を横(x),被説明変数とする方を縦(y)に据え,関係を明確にしておくべきでしょう。
グラフの書式を任意に整えます。
ここでは,次のような点を調整しました。
- グラフタイトルを削除
- プロットエリアを正方にしたうえで枠線を描画
- 目盛間隔の修正と目盛線の削除
- マーカー(ドット)のサイズを少し拡大
- マーカーが多いので,それらが重なって潰れると区別がひときわ難しい マーカーの塗り色と線色を異にして判別を容易に

この散布図を一瞥した感覚では,2つの変数には直線的な関係があることが窺えます。ま,なんとなくですけど。
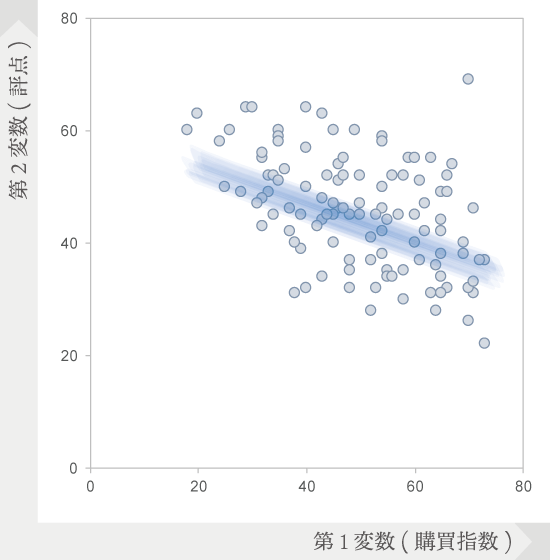
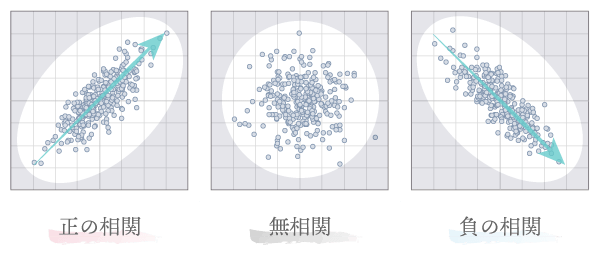
「直線的な関係」について,右上がりのものを正の相関,右下がりのものを負の相関といいます。翻って,そうした関係が見られないものを無相関と呼びます。
正の相関は,すなわち“第1変数が増加すれば第2変数も増加する”という関係が,負の相関は“第1変数が増加すれば第2変数は減少する”という関係が互いの変数にあることを意味します。
Extension
元データの性格(2変数が明瞭に正規分布にしたがうような)次第で,ふつうに散布図を描くより,データを標準化してから描く方が有効な場面があります。このエクステンションでは,データの標準化を経て散布図を描く手続きに触れながら,後述のPearson関数によって求められる相関係数の中身(式の内容)について見ていきたいと思います。
READ MORE
標準化のメリットとその作業
散布図を作成すると,“2変数の関係が直線的なものかどうか”と,そうであるなら“正の相関がありそうなのか・負の相関がありそうなのか”についてを知ることができます。ただ,後の工程で求める相関係数を散布図から「だいたいこのくらいかな」と推し量るのには少し注意が必要かもしれません。
確かにある特定の変数について,定期的に相関を観測しているようなときには「いつもと同じ変数だし,前提も変わらず ましてやさしたる状況の変化も感じなかったし前回の相関係数が0.4だったからこの分布だと今回は少し上の0.5くらいかな?」と散布図だけでおおよその判断をつけられる場合もあるでしょう。
ですが現実の話としては,分析下の環境や対象がそうした単純かつ固定的な状況にあることが確約されるはずもなく,また人によっては目盛りの取り方に“クセ”のようなものが強く出たりもします。そうした点に思い当たると,相関係数と散布図の形状は,ここで「一意に結びつく」と明言してしまうのもある意味では危険かもなんて,わたし的には思うところもあります。
たとえば,ここまでの過程で描いた散布図について,片方の軸だけ目盛のとりかたを変えてしまえば,形状は下の図のよう変貌します(下方の2つ)。
ここで善意の読み手に対し,目盛のとりかたを変えた事実を伏せてこの図を開示したとします。この善意の読み手の何人かは,見た目の密度の高さに気を取られ,真のものより高い相関を推察するなんてミスリードが成立する可能性を否定できません。

翻って考えると,スケールを統一してしまえば,分布のかたちと相関係数とのつながりも,より密なものにできそうです。
とりわけ,単位の大きく異なるデータを扱うときや,予測しがたいムラの大きなデータを扱うとき(いずれも目盛のとりかたを統一・維持していくことが難しいケース),あるいは2群ないし2時点間での分布のかたちを比べてみたいときには,2変数のスケール調整が有効な場面も多いように思います。
ということで,ここからしばらく,そうした対処のひとつ: データを標準化してから散布図を描くプロセスを挟んでいきます。この形式の散布図は,ふつうの散布図との比較に言えば,平均および1標準偏差を示しうるという意味で情報量を増やしたり,あるいはスケールの揃った4象限マトリクスにスッキリ・スマートにデータを落とし込めるといった,いくつかの利点を持ちます(後述)。
ではでは 任意の場所に見出し平均標準偏差およびzXzYを用意します。
ここで zは標準得点(z-socre)を指しています。D列のzXは「購買指数」の,E列のzYは「直近の評点」のそれです。
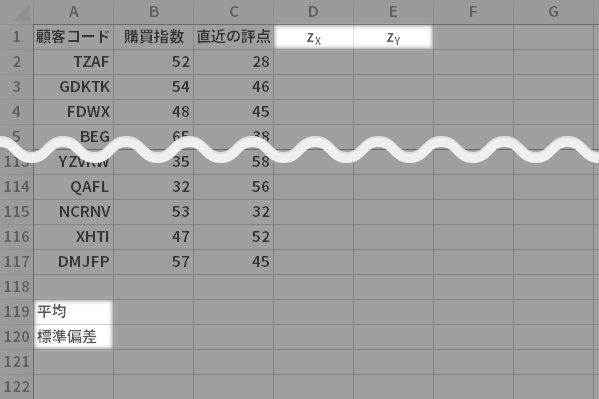
2つの変数(購買指数・直近の評点)について,平均と標準偏差を求めます。
具体的に,まず1番目の変数について以下を順に入力し,
- =AVERAGE(B2:B117)
- =STDEV.P(B2:B117)
これらを2番目の変数の列にもコピーします。

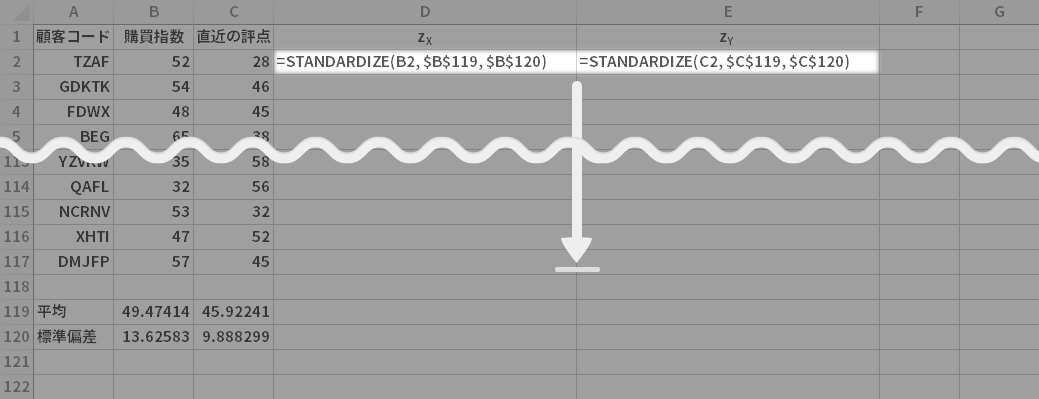
Standardize関数を使って両変数の標準得点を求めます(標準化)。
具体的には,絶対参照の部分に注意して,
- CELL D2=STANDARDIZE(B2,\$B\$119,\$B\$120)
- CELL E2=STANDARDIZE(C2,\$C\$119,\$C\$120)
と入力し,ともに最下行までコピーします。
Standardize関数の「関数ウイザード」を使った入力方法は,必要であれば偏差値表の作成頁を参照のこと。
共分散と相関係数
あせっかく標準化という処理を挟んだので。
それと密接に絡むお話あとから出てくる相関係数の中身(計算のしくみ)についても,少しだけ加えておきたいと思います。
標準化を経た「購買指数」および「直近の評点」のいずれも,平均が0,標準偏差が1のパラメーターをもつ変数となっています。
ここで「平均が0」であることに着目すると,標準得点は,おのおのの顧客IDが得た変数の値が“平均からプラス方向あるいはマイナス方向にどれだけ(標準偏差何個分)離れているか”を示していると解釈できます。
SEE BELOW
- 偏差 ―"Wikipedia"
そして,これらの標準得点について
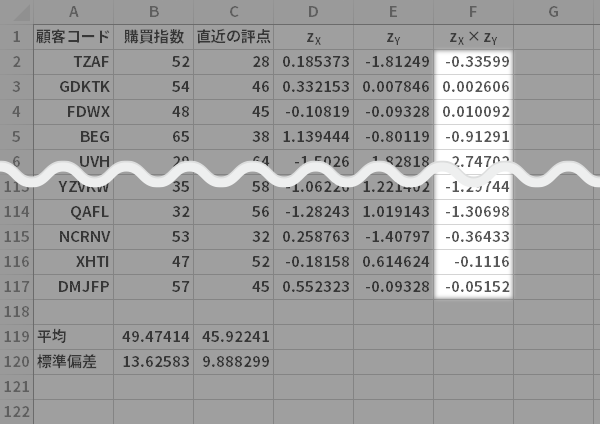
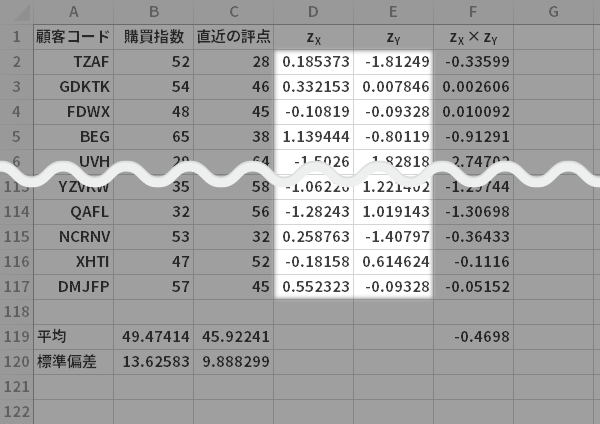
下の図のように先頭の顧客の「zX」「zY」をzX×zY列で乗じてやると,偏差積と呼ばれる値が求まります(ハイライトの部分)。
これをすべての顧客について計算(データのサイズ$n$個分)していくと
現実的にはセルF2の計算式を表の最下行までコピーします。

こんな感じになりました。
ってことで,今度は,このハイライトの部分の総和(偏差積和)を$n$で割ってみちゃったりしたいと思うのです。言い換えれば,これは偏差積の平均を求めることですから
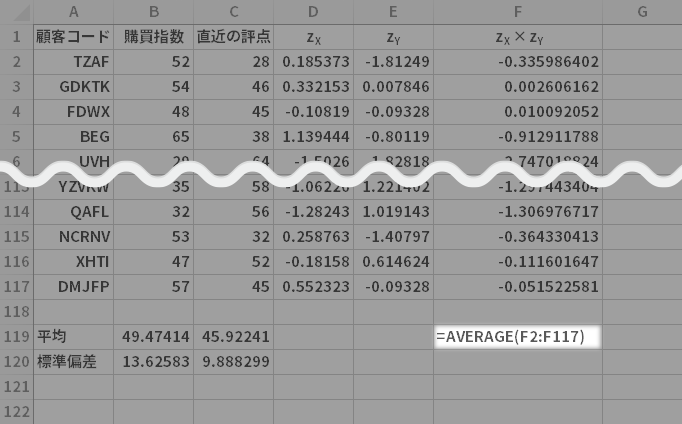
下の図のようにAverage関数を使えば簡単ですね。
というわけで,このAverage関数の戻り値のことは共分散と呼ばれます(下の図ではセルF119)。
ただし$n$でなく$n-1$で除すタイプもあります。
Excelには共分散を直接計算できる関数があります。この場合,標準化してある・ないは関係なしにCoVariance.p($n$で除す場合), CoVariance.s($n-1$で除す場合)の各関数が利用できます。いずれも引数には2つの変数を指定します。
SEE BELOW
- 共分散 ―"Wikipedia"
唐突なようですが,このページで相関係数(ピアソンの積率相関係数: $r$)と呼ばれるものは,下に示された式から求めることができます。
上で求めた共分散というものが,実のところ相関係数を求める上でかなり重要な要素となっていることがわかります。
さて,この式によれば相関係数は,共分散を両変数の標準偏差の積で割って求めます。先に触れたように両列の標準偏差は標準化しているのでともに1であることは自明です。つまり,2つの変数を標準化した場合は,分母は必ず1となるので相関係数=共分散の関係が成り立ちます。
この点を鑑みれば,このあと触れる相関係数と呼ばれるものは,“標準化された共分散”と考えても分かりやすいかと思います。

前後してごめんなさいですけど,ここからふたたび標準化したデータを使って散布図を描く話に戻ります。
では,「zX」列と「zY」列のデータを見出しを除きすべて選択します。
リボンの挿入タブグラフグールプにある散布図(X, Y)またはバブルチャートの挿入ボタンをクリックします1。
つづいて プルダウンメニューの散布図ボタンをクリックします2。
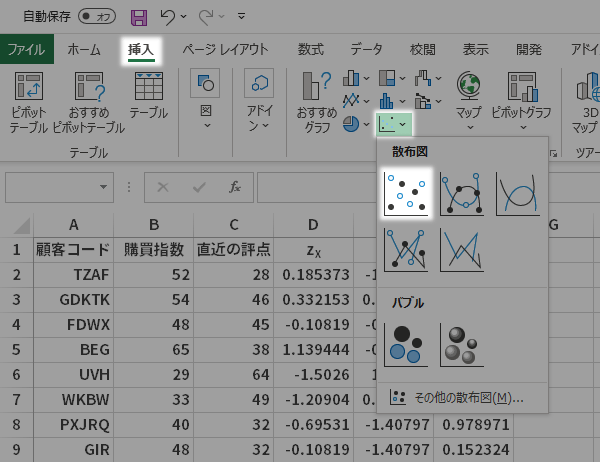
DIFFERENT VERSIONS
1 2010: 挿入タブグラフグールプにある散布図ボタン
2 2010: 散布図(マーカーのみ)ボタン
シートに散布図が差し込まれました。
とりあえず,ここでは5でしたように,グラフタイトルを削除したうえで,マーカーの書式だけちょろっと触っておきたいと思います。

DIFFERENT VERSIONS
2010: グラフタイトルが挿入されない代わりに,凡例が差し込まれます。散布図の場合,層別グラフでもない限り凡例の必要性も高くはないので,凡例を直接選択しDeleteキーで消去します。
グラフの横軸・縦軸とも最大値・最小値を揃えます。この例では,横軸最大値が他と異なっていますので合わせていきます。
グラフの横軸を選択し,書式タブ現在の選択範囲グールプにある選択対象の書式設定ボタンをクリックします。
スケールを固定して異なる条件・時点で観察する
正規分布を仮定した場合,±3標準偏差にほとんどのデータ(99.7%)が入ります。したがって(別途外れ値の有無に関する関心は必要ですが)おおむね定型的に min:-3, max:+3 あるいは min:-4, max:+4 あたりの設定でカバーできると思います。
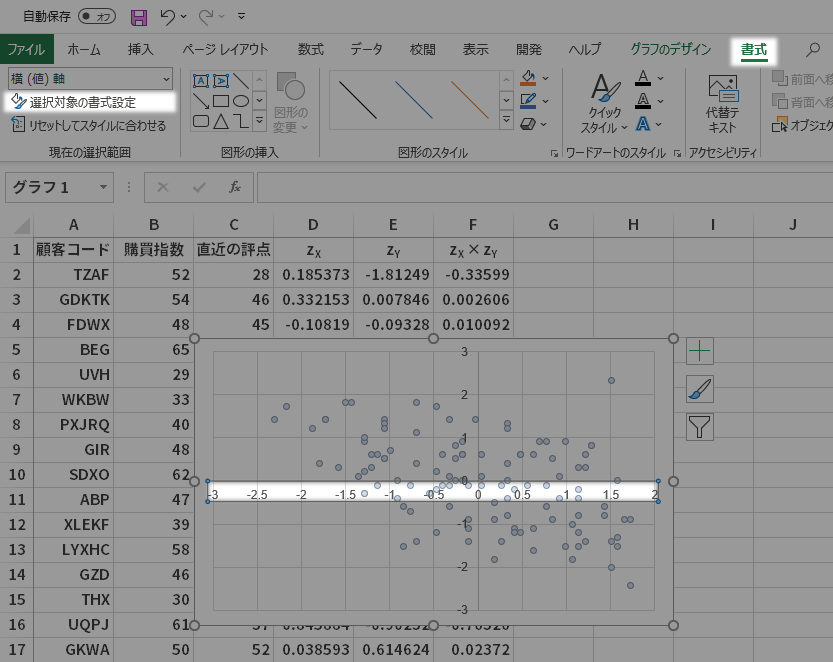
DIFFERENT VERSIONS
2010: 選択対象の書式設定ボタンはレイアウトまたは書式タブの中にあります。
軸の書式設定ダイアログが表示されます。
下の図のように,境界値の最小値最大値にはこの時点のグラフの目盛の上限・下限等に鑑みて適切な値を(この例では順に-3, 3とします),単位の主には1を入力します(なお,グラフの上では適切な数値となっているはずの最小値と目盛間隔をここであえて指定するのは,意図しない図のくずれに対する予防策的な意味合いからです)。
加えて目盛の種類を交差に変更します。
もう一方の軸も同様に調整を済ませます。
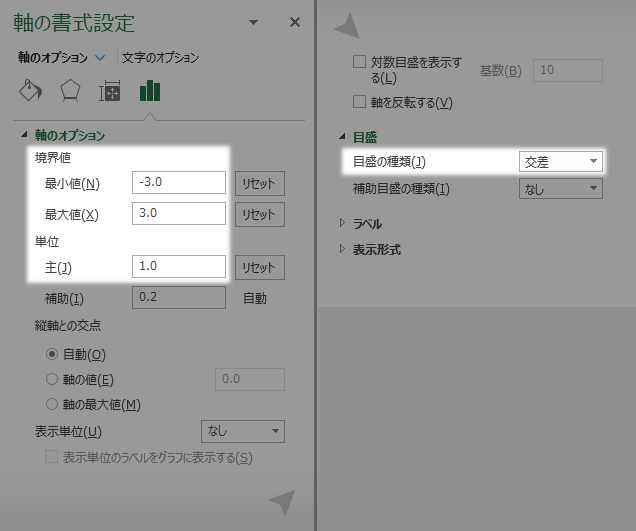
DIFFERENT VERSIONS
2013, 2010: [変更前の表記]目盛間隔。
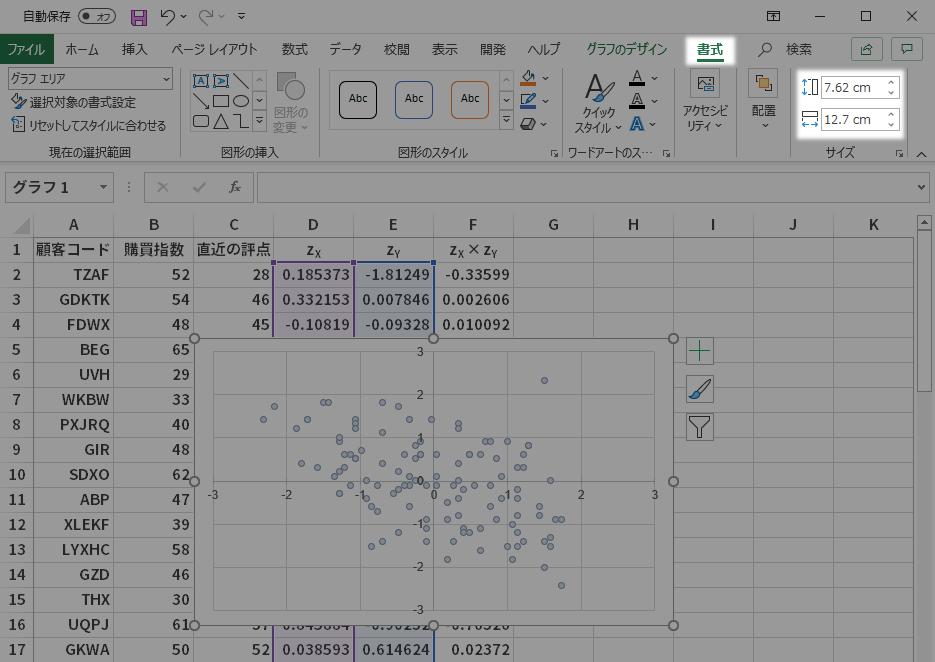
グラフエリアがアクティブになっているか確認します。
アクティブな状態を維持しつつ,サイズグールプの図形の高さ,図形の幅を任意の等しい値にするなどして,グラフができるだけ等比となるよう調整します(たとえば高さ10cm・幅10cmのように指定)。
px単位でも指定できます。
平均で仕切る4象限のマトリクス
Extensionで意図した散布図が用意できました。縦軸・横軸の中心のラインは,それぞれの変数の平均(=0)です。また目盛1つが1標準偏差(=1)です。
両軸のラインを基準に区別可能な4つの区画は象限と呼ばれ,下の図のように右上がともに正の値となるような目盛をとるとき,右上から順に,反時計回りで第1象限,第2象限,第3象限,第4象限と呼んでいきます。
| 象限 | xの標準得点 | yの標準得点 | |
| 1 | + | + | ともに平均より高い |
| 2 | - | + | yのみ平均より高い |
| 3 | - | - | ともに平均より低い |
| 4 | + | - | xのみ平均より高い |
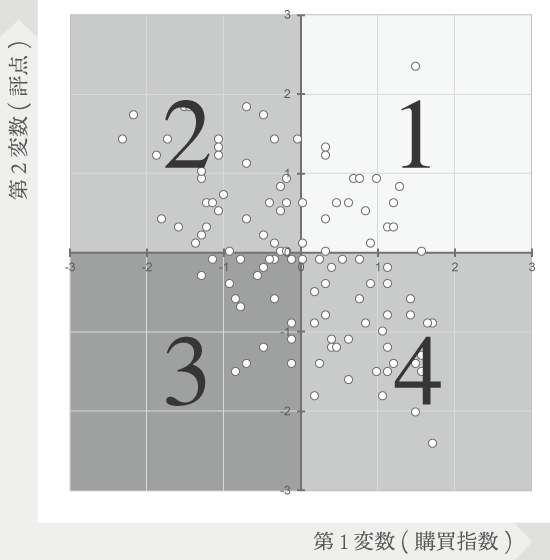
ざっくりと言えば,この象限1と3,ないしは2と4のどちらにより多くの要素が集まるかで,相関係数の符号が決まります(より忠実には,先に見た偏差積の和を1・3象限[+側]および2・4象限[-側]の別にとったとき,いずれの側が符号を決める力をもっているか[絶対値で大きいか])。前者の場合プラス(正の相関),後者の場合マイナス(負の相関)となります。
ここでは下のように2・4側により多くの要素が集まりましたからマイナスですね。
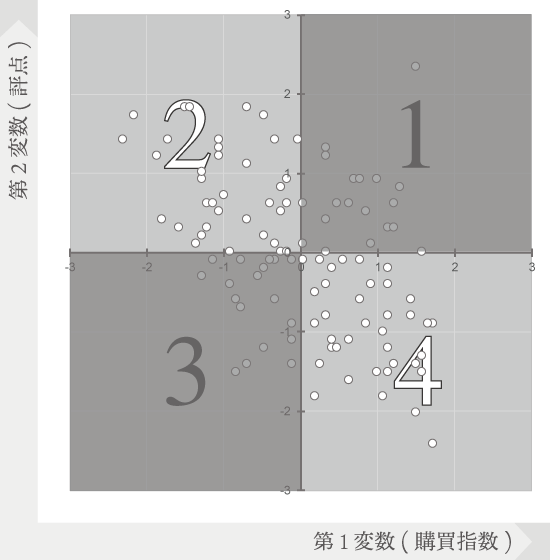
この構成の散布図は4つの大きなセルを持つことから,ポジショニング,あるいはセグメンテーションのツールとして平易で,ある種のコンセンサスもある「4象限マトリクス」として準用することが可能です。
たとえばこの例では,2変数それぞれの意味において第1象限から第4象限まで下のような名前をつけ,セグメントごとにより相応しい施策を管理するといった活用のしかたが浮かびます。この場合,マクロを使って要素にラベル(ここでは「顧客コード」)を表示させてやれば,一覧性を高めることができるかもしれません。
SEE BELOW

「外れ値」を考える
ここで最初のExtensionを終えて,頁頭でしていたふつうの散布図の話に戻りたいと思います。
えーと先の散布図からは負の相関の存在が察せられたので,今度は散布図のこの部分(ハイライトの部分)に注目したいと思います。
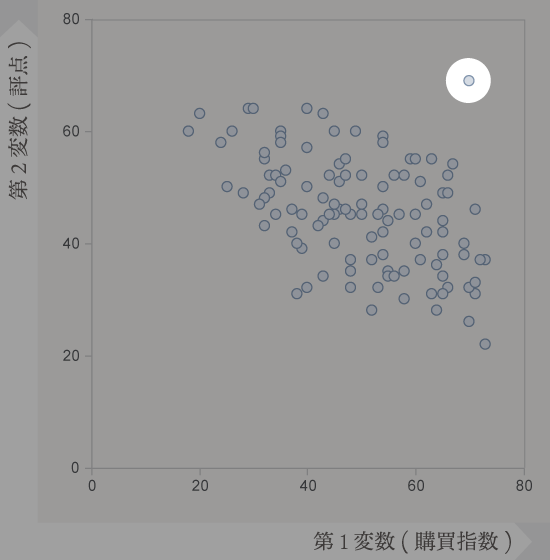
1つだけ,マーカーの密集しているエリアから目立って離れたところにデータが存在しているのがわかります。これを外れ値といいます。この外れ値が,何らかの特殊な事情をもっている(異常値)のか,検討したほうがよさそうです。
というのも,外れ値は,後の工程で求める相関係数に強い影響を与えます1。他のデータと馴染みがたい異常値であることが色濃くなったとき,検討次第でデータの塊から除外する選択も出てきます。
私が欲しいのは,単なる“計算したら出てきた値”じゃなくて,実情がよく斟酌された値のハズですから,異常値の可能性を探ることにとても重要な意味があります。外れ値の検出法としては,もちろん統計学的手法を利用するものもありますが2,“違和感”を判じるのが得意な人間の視覚こそ第一義だと考えます。
SEE BELOW
- 1 クレーム入電件数の平均
- 2 e.g. マハラノビス距離の2乗
そこで一旦作業を中断して,この顧客を調べます。
私のことなので,そもそもデータの入力ミスかも知れませんし。
えーと,顧客コードLMCPAのお客さんのは入力ミスじゃない。ん!? どうやら社長自らイレギュラーにフォローしているよう。
結局,ウチの社長と深く関係のある会社さんで,他のお客さんと比べきわめて特殊な形態で取引している先であることが分かりました。今回の分析の前提とは相容れない(と考えてください)ということでこれを“除外すべき”異常値として認め,データから外すことに決めました。
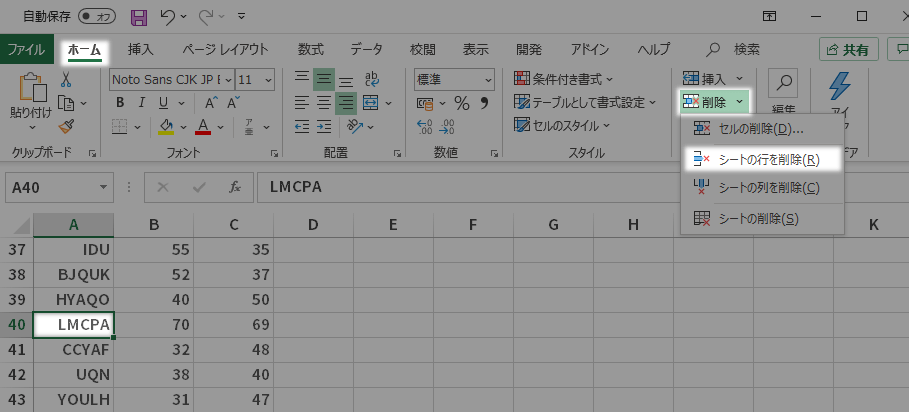
ということで除外の対象となったこのデータはえーと40行目にありました。これを行ごと削除します。
具体的には,40行目の任意の列をアクティブにした状態から,セルグループの削除メニューでおこないます。
散布図が下のように自動的に修正を反映します。
ここまでに軸の最大値・最小値の設定を経ていない場合,削除したデータによってはそれらが自動で再調整されることがあります(この例では縦の最大値が8070のように)。これについて不都合のある場合,必要に応じて適切な設定を加えます。
以上で散布図は完成です。

相関係数を求める
大きな流れの第二として,相関係数を求めます。
シートの空いているところ(ここではセルE1)に,あたらしい見出し相関係数を作成します。
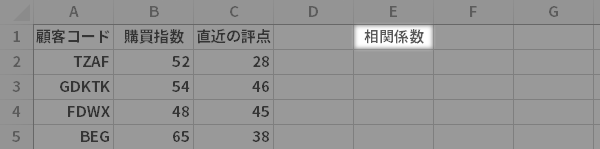
そういえば,すこし脇道にそれちゃいますけど,一口に「相関係数」と言っても,あいまいな意味ではいろいろなものがありますね。
えーと元データの2つの変数がともに数量(間隔尺度・比尺度)であり,直線的関係が見られる場合は,ピアソンの積率相関係数(単相関係数)を用います。このページの例でも変数はともに数量(間隔尺度)ですから,ピアソンの積率相関係数を求めることができますね。Excelにはこれを計算するための組み込み関数があります。
参考として,その他
2つの変数が数量データ(間隔尺度・比尺度)とカテゴリデータ(名義尺度)の場合の“相関係数”として相関比が,ともにカテゴリデータ(名義尺度)の場合にはクラメールの連関係数が,また,とりわけ順序尺度の場合にはスピアマンの順位相関係数といったものが利用されたりしますです。
スピアマンの順位相関係数
(1)異常値の判断がつかなかった場合など外れ値を含んだまま相関係数を求めるようなとき,それによる影響をできれば除きたい (2)2つの変数が正規分布にしたがうという仮定をおかない …といった状況下で選択されることが多いです。
先ほど作成した「相関係数」見出しの直下のセルをアクティブにし,数式バー横の関数の挿入ボタンをクリックします。
関数の挿入ダイアログが開きます。
関数の検索ボックスに "pearson" と入力し,検索開始ボタンをクリックします。
Pearson関数とCorrel関数
この記事の最終更新時点でMicrosoftのサポート対象となっているExcelのバージョンでは,いずれの関数でも同じ結果が返りますので,ここではCorrel関数を用いてもOKです(Pearson関数 ―"Office")。
もっとも関数"Pearson"の字面はピアソンの相関係数を想起させるに有用なので,このページではPearson関数の方を明示的に利用しています。
関数名のいちばん上に,目的の「PEARSON」が表示されていると思います。
こちらを選択し,OKボタンをクリックします。
関数の引数ダイアログの配列1配列2の 2 カ所について,下のようにシート上の対応する色のセル範囲(各列の見出しを除くすべてのデータ)を指定します。
すべて入力した後,OKボタンをクリックします。
散布図の作成と相関係数の計算,完了です。
あ,えと,念のため相関係数「-0.52点」「-0.52ポイント」とかいったように,勢いあまって相関係数に単位をつけちゃうのはNGなので注意です。
無名数・順序尺度
相関係数そのものは単位を持たない無名数として扱います。またこれは,順序尺度となります。
後者の点についてここで少し顧みておきたいと思います(cf. 順序尺度「尺度水準」 ―"Wikipedia")。たとえば同じ2つの変数の相関係数を過去2つの時点にわたり観測してきたとして,その内容が以下の通りであったとします。
0.2, 0.4
このとき,直前のものを評価するとして,順序尺度は大小のみが意味を持ちますから
- 前時点より「強く(大きく)なった」
ことを言うことは可能なことがわかります。反面,加減乗除($+-{\times}\hspace{.2em}{\div}$)に意味はないので,第一として
- 前時点より200%(2倍)強い
とする表現を用いることが適切とは言えなくなります。またさらに,その後の観測値が
0.6
であったとしたとき,第二として
- 直前との比較で0.2ずつ増加してきたすなわち,等間隔で均等に強くなってきた
とする表現も不適切となることが分かります。

Extension
この頁の事例は標本を対象としたものではないことから,相関分析のための手続きは以上で完了としています。ここからは仮のお話として,元データが標本であった場合の検定(無相関の検定)と推定(母相関係数の推定)について加えたいと思います。
READ MORE

無相関検定
少し補足します。その前に,ここからは仮のお話ですので前提を崩しちゃいます。
今回分析対象としたデータがより大きな母集団から無作為に抽出した標本だったとして,先のような相関係数:-0.52を導いたと仮定します。
この場合,実際には2つの母集団が無相関(母相関係数$\rho=0$)であったとしても,きわめて希な組み合わせで相関の見られる標本となってしまうケースもあります。そこで相関があるかないかのひとつの判断として,無相関検定をおこなってみます。
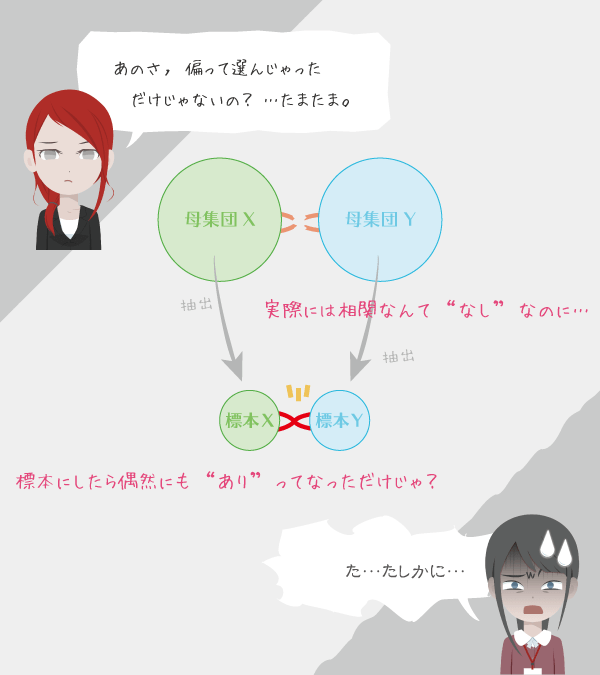
検定ということで,何よりも仮説がなければ始まりません。帰無仮説と対立仮説は次のようにしておきます。
- 帰無仮説(捨てたい仮説)2つの母集団の相関係数はゼロ。
- 対立仮説(採用したい仮説)2つの母集団の相関係数はゼロでない。
また,データ対の数,自由度,そして先に求めたピアソンの積率相関係数は,次のとおりです。
- データ対の数$n$ : 115
- 自由度$df$ : 113($n$より変数2つ分を減らし$n-2$とします)
- ピアソンの積率相関係数$r$ : -0.52

検定統計量$T$を求めます。式は下のとおりです。
シートの空いているところを使って,上で示した値を式にあてはめて計算してみます。

とはいえ,上の式の入力はちょっと繁雑ですね。よってここでは分子と分母に分けて計算したいと思います。
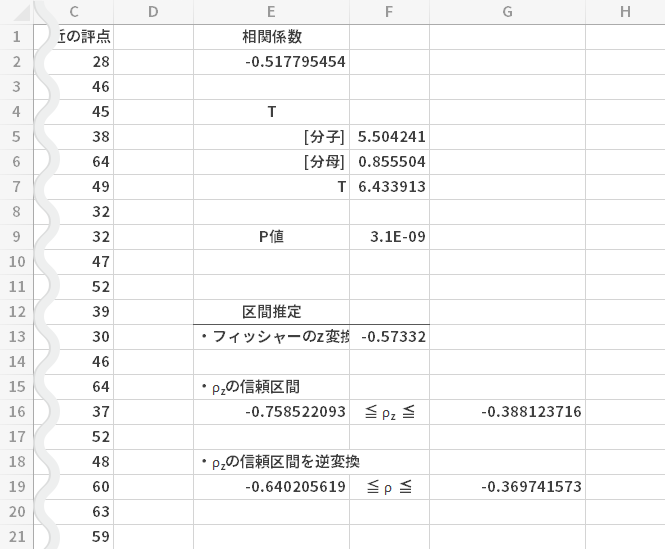
下の図のようなシート構成のとき,分子・分母・そして$T$の計算式は次のようになります。
- CELL F5: 分子=ABS(E2)*SQRT(115-2)
- CELL F6: 分母=SQRT(1-E2^2)
- CELL F7: T=F5/F6

$T$はおよそ6.43となりました。

この$T$の値と,$df$を使って有意確率($P$値)を計算します。無相関検定の場合,帰無仮説こそ正しい!とする前提下なら,$T$は $df=n-2$ の $t$ 分布 にしたがうばずなので,両側の$P$値をT.Dist.2T関数で求めてみます。
ここでは,先にPearson関数を使用するときに呼び出した関数の挿入ダイアログを再び使って入力していくことにします。したがって,空いている適当なセルをアクティブにし(ここではセルF9),関数の挿入ボタンからT.Dist.2T関数のダイアログを呼び出します。
関数の引数ダイアログのXについて,下のようにシート上の対応する色のセル($T$の値)を指定します。
つづいて,自由度は $n-2$ ですから,この例の場合は113と指定します。
すべて設定した後,OKボタンをクリックします。
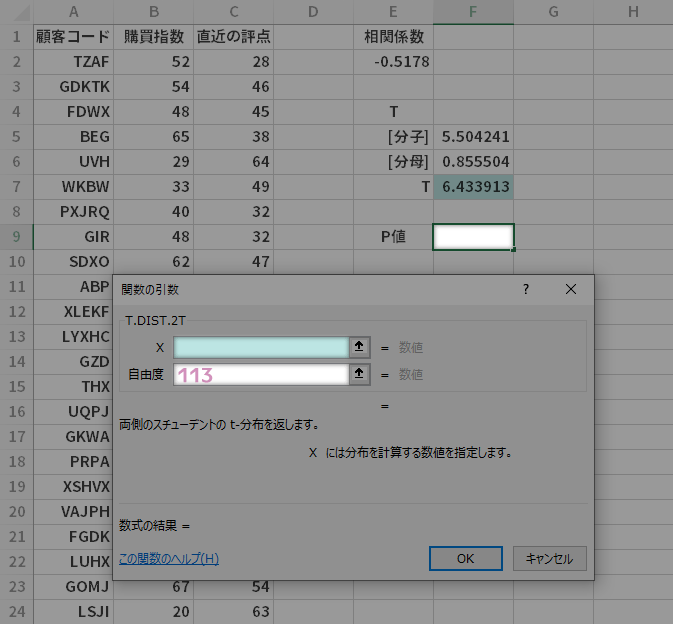
$P$値には「3.10192E-09」と表示されています。これは指数表記です。
参考までに通常の表記になおすと「0.000000003…」といったところです。
すなわち,有意水準($\alpha$)が 5%(0.05), 1%(0.01)いずれであったとしても$P<\alpha $となり,帰無仮説が棄却されます。つまり,2つの母集団の「相関係数はゼロではない」と考えることができます。

母相関係数の信頼区間の推定
これによって,たしかに“(程度を問わず)相関がある”ことを補強できたとは思います。が,あえて重箱の隅をつつくような真似をするなら,対立仮説「母集団の相関係数はゼロではない」については,ゼロでなくても |0.1| や |0.2| の可能性を少なくとも否定してはいないじゃん!?なんて思ったりもします(先に掲げた$T$を求める式: “分子に$n$がある” サンプルサイズが大きければ$r$が小さくても有意になる)。
この点については,発表等の場において当該結果を評価者の耳目にさらすことになると,えてしてツッコミが返ってくることも少なくない部分のような私自身は,そんな感触をもっています。
そうした点をふまえれば,“母相関係数がゼロでない”ことを言うよりも,“母相関係数はこの範囲のどこかにあると推定できますっ!”なんてことを言えた方が何かと都合がいいのかもとも思えてきます。以下,しばらくそのための手続きです(母相関係数の信頼区間の推定)。
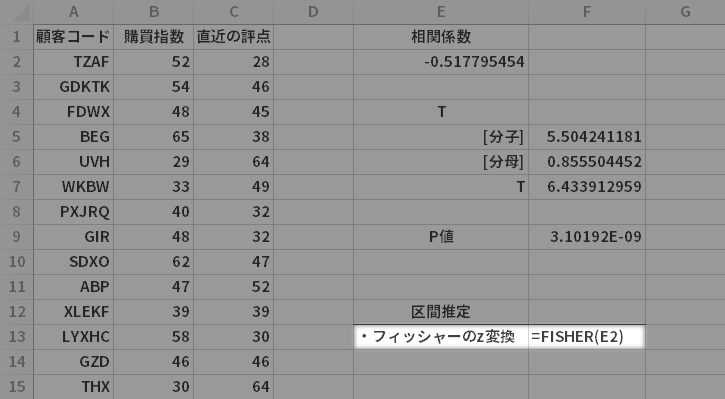
(標本)相関係数$r$をフィッシャーの$z$変換と呼ばれる方法で標準化します(パラメータ [平均] ${\raise.2em 1}{\lower.5ex \Large/}{\lower.2em 2} \cdot \ln{\{{\raise.0em {(1+\rho)}}\hspace{.2em}{\lower.5ex \Large/}\hspace{.2em}{\lower.0em {(1-\rho)}}\}}$,[分散] ${\raise.2em 1}{\lower.5ex \Large/}{\lower.1em {(n-3)}}$ の正規分布に近似的にしたがうようなかたちに変換)。
- =FISHER(E2)
(以下,計算のしくみを明らかにしておきたい場合の選択)
- =1/2*LN((1+E2)/(1-E2))
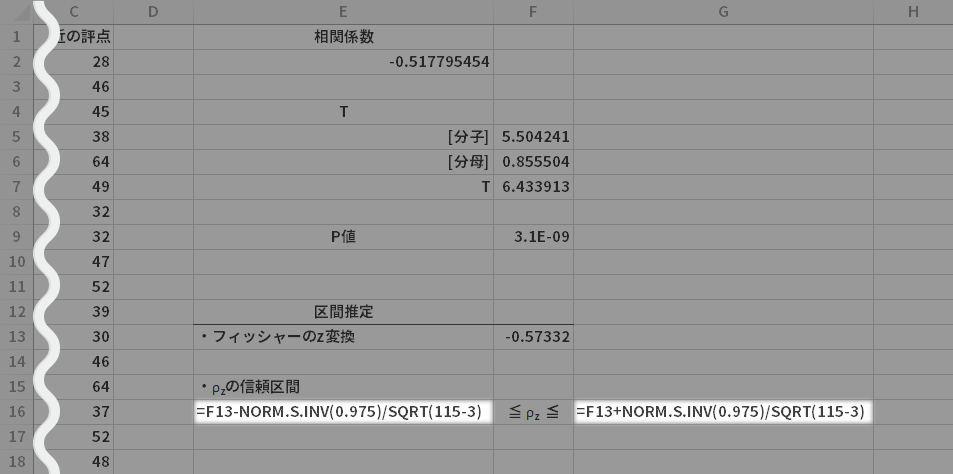
上で求めた値($r_z$)に ${\raise.2em {z(\alpha/2)}}\hspace{.5em}{\lower.2em \Large/}\ {\lower.2em {\sqrt{n-3}}}$ を加減して,変換値による母相関係数($\rho_z$)の信頼区間を求めます。なお下式にいう$z(\alpha/2)$は標準正規分布の上側$\alpha/2$パーセント点とします。

ここでは信頼区間を信頼度95%,つまり$\alpha=0.05$で求めるものとします。ということで,先の式の$z(\alpha/2)$は2.5%点の値が必要なのでこれをNorm.S.Inv関数によって求めます(ただし引数は下側[累積]確率を求められるので0.975)。
式をシートに具体的に入力すると,次のようになります。
- 下側=F13-NORM.S.INV(0.975)/SQRT(115-3)
- 上側=F13+NORM.S.INV(0.975)/SQRT(115-3)
$\rho_z$を$\rho$に戻します(逆変換)。
- 下側=FISHERINV(E16)
- 上側=FISHERINV(G16)
(以下,計算のしくみを明らかにしておきたい場合の選択)
- 下側=(EXP(2*E16)-1)/(EXP(2*E16)+1)
- 上側=(EXP(2*G16)-1)/(EXP(2*G16)+1)

母相関係数の信頼区間は-0.641~-0.369となりました。先の検定でみたとおり,この範囲にはゼロが含まれていないことを確認できます。
ただし信頼度95%としたので,同じ母集団から無作為に20回標本を抽出して信頼区間を求めてみるとして,真の母相関係数がうち1回だけは計算によって求められた範囲から外れる程度の確からしさとなります。

以上,あくまで元データが標本であることを仮定した場合のお話でした。ストーリーパートの方ではそうでない場合は,このような検定や推定をする必要はないですよぉ。






