最近隣法による単純予測 with Excel

2023/7/10

イントロダクション

「ナイーブ(naïve)な予測」とは，次の1期の定量的な予測値を用意する必要に迫られたとき，直前の実測値をそのままスライドさせて“予測値”に充てる方法を指します。ここで扱う方法はその単純さを踏襲しつつも，「そのまま」ではなく再近隣法による合成値を使います。

念のため，ここにいう「ナイーブ」は，英語圏でいうネガティブなニュアンスを保持したものです。予測という行動にシャープな論理性を同伴させる目的では薄弱ですが，裏を返せば理解しやすいシンプルなしくみであることから，「予測」といったものを何らの手段で出さなければならないときに，ユーザーが他にノウハウを所持していなければ，取っ掛かりの容易さという意味では最も利用しやすい部類の方法と言えます。

最近隣法で特徴的といえるのは，ある“パターン”を探すことです。これを予測に準用するとき、直近にあらわれたパターンを過去のデータの蓄積に照らしあわせて，適当な実測値に重みづけをおこない，その総和をとって予測値を導きます(仔細は文中で触れます)。

また制約としては，別頁の単純予測(移動平均法，指数平滑法)の場合と同様，

計算に利用する観測値のmaxを超える，あるいはminを下回る値を予測値として出すことはできない。

を抱えます。

以下，Excelによる再近隣法を使ったナイーブな予測の流れです。ここでは一連の手続きを Excel 2016 で追っています。一部ボタンの配置や名称などが異なる箇所がありますが(この場合，可能であれば当該箇所に明記します)，手続きそのものは，「永続ライセンス版」にいうところの Excel 2019, Excel 2013 あるいは Excel 2010，そして，「Office365版」の Excel (本頁更新時点のver.1905)でも基本的には同じです。

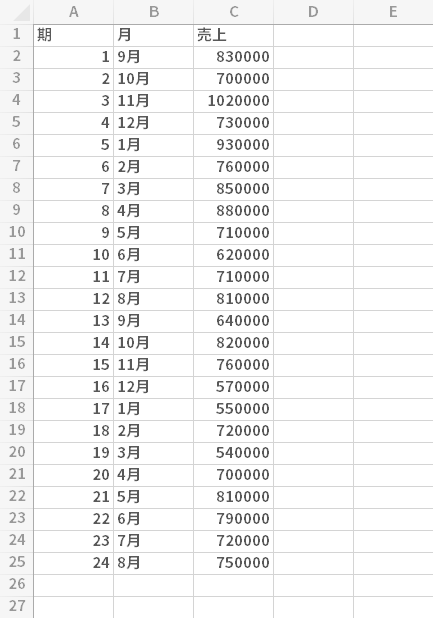
元データ

元のデータです。

左の「期」列はデータの数を分かりやすくするため便宜的に挿入したものです。ですので処理上，なくてはならないもの！というわけではありません。

このデータより25期目(9月)の売上の予測値をつくるのが目的です。

直近のパターンに似た過去のそれを探る

あたらしく見出しを作ります。

「売上」列の右隣から順に，2期前の売上1期前の売上距離距離の逆数順位ウエイト売上×ウエイトと入力します。

ぶっちゃけ，これらの列は計算のプロセスを適度に分類しただけのものです。個別の列それぞれに独立して大きな情報を示すものではありませんので，見出しそのものもポイントを外した点があることは含めおいてください。

[セルD1]2期前の売上, [セルE1]1期前の売上, [セルF1]距離, [セルG1]距離の逆数, [セルH1]順位, [セルI1]ウエイト, [セルJ1]売上×ウエイト

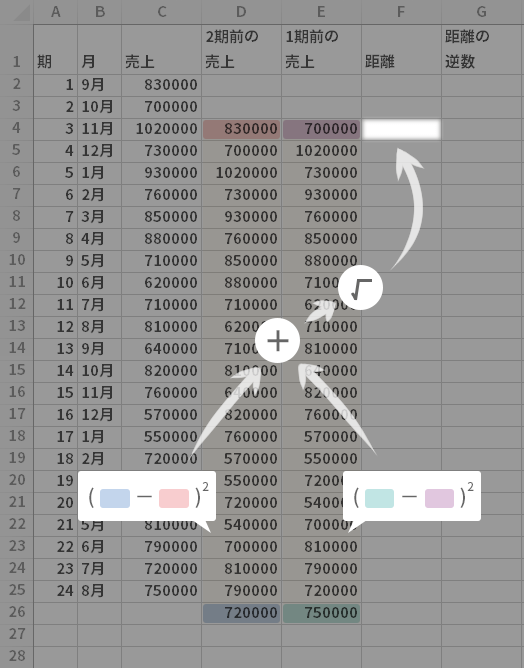
では，「2期前の売上」列と「1期前の売上」列をあわせて用意します。

2期前の売上・1期前の売上ともにデータが揃うところつまり，両列とも3期目からの入力とします。

ということで，下のように「売上」列をそのまま転記する式を入力します。

入力できたら，両列の計算式を表の最下行より1つはみだすところまでコピーします。

次に「距離」列を計算します。

この列には，下の図のような構造の式を用意していきます。

はたしてこれで何をしているのかと言えば，下の上段の図にいう赤い線ライクなパターンを探しています。

イメージとしては，この赤い線の両端に下の下段の図のように線を引き

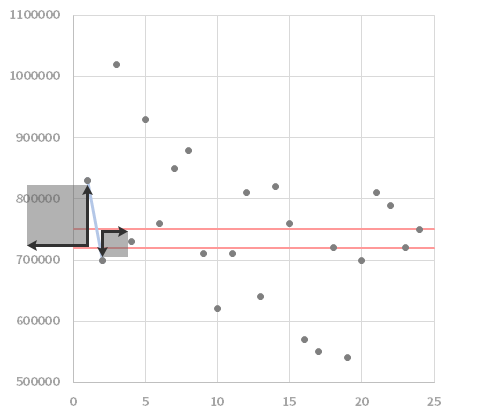
それらから売上までの距離を，下の上段の図にいう左端から順にペアで走査していきます。このとき，黒い線がその「距離」を示します。

この距離は向きが異なると足し合わせた際に相殺されてしまうので，分散を計るときのように2乗つまり下の下段の図のような黒い正方形の面積を考えればいいわけですが，これを足し合わせたものがどれだけ小さいかで，5の上段の図で掲げたパターンと近しいことを見当づけることができます。

なお，“面積”のままでは以下での扱いが面倒なので，ルートをとって最後に単位を戻します。

ということで上述の意図をかたちにしたものが下式です。これを「距離」列，上から3番目のセルから入力していきます。

=SQRT(($D$26-D4)^2+($E$26-E4)^2)

入力できたら，これを「1期前の売上」列の最下行と同じ行までコピーします。

[セルF4]=SQRT(($D$26-D4)^2+($E$26-E4)^2)。この式をセルF26までコピー

「距離の逆数」列を計算します。この列は“重み(ウエイト)”として利用します。

先に見たように，「距離」はパターンが近ければ小さくなる関係にあるので，これをそのまま重みに充てるとができません。そこで，この逆数をとることで大小関係を逆転させます。

具体的には，上から3番目のセルに

1÷距離

となる次の計算式を入力し，これを24期の行までコピーします。

=1/F4

「順位」列を計算します。これにより近しいパターンのものをいくつか，順位(昇順)をもとに拾い上げるしくみの端緒とします。具体的には，上から3番目のセルに，次の計算式

=RANK(F4, $F$4:$F$25, 1)

を入力します。このとき，ランクづけの対象範囲は下の図でいうシート上の青の囲み部分となります。0(黄色のバツ印)のセルは含めません。

入力できたら，式を24期の行までコピーします。

(Rank関数 ―"Office")

[セルH4]=RANK(F4,$F$4:$F$25,1)。この式をセルH25までコピー

候補より “次に測定された値” を拾って合成する

ここで表の右端にいったん視点を移します。

「売上×ウエイト」列の右方に1列あけて，あたらしい見出し採用期数と，そのとりあえずの値6を入力しておきます。

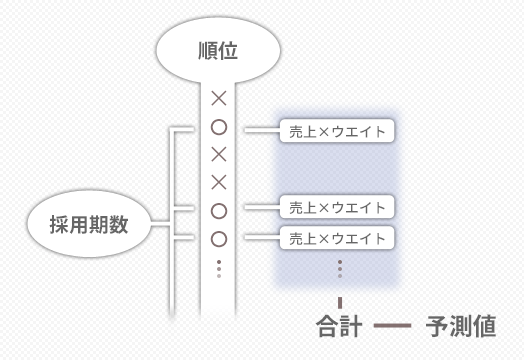
この「採用期数」をもとに，この後のプロセスで下の図のような処理ができるよう表をととのえていきます。

具体的には，まず①採用期数の分だけ，予測に利用するレコード(行)を特定します。この特定にあたっては，順位の昇順(1位からの順)で決めていきます。

そして，②該当するレコードの売上(実測値)に重みを掛け合わせ，最終的にそれらを合成することによって予測値を作成します。

「ウエイト」列を計算します。上から3番目のセルに

=IF(H4<=$L$2, G4/SUMIF($H$4:$H$25, "<="&$L$2, $G$4:$G$25), "")

と入力します(この例では何も表示されませんが正常な処理です)。

入力できたら24期の行までコピーします。

(Sumif関数 ―"Office")

[セルI4]=IF(H4<=$L$2,G4/SUMIF($H$4:$H$25,'<='&$L$2,$G$4:$G$25),'')。この式をセルI25までコピー

この一見ややこしそうな式は次のような構造になっています。

ことばで示すと，「順位」列の値が「採用期数」で指定した値以下の順位であれば，下の着色部分の式で重みを案分し，そうでなければ空白処理をするといったところです。

残る「売上×ウエイト」列を入力します。これは見出しの文字の意味するところそのままの式で求めますので，上から3番目のセルに

=IFERROR(C4*I4, "")

と入力します。ただし，左隣の「ウエイト」列にデータがないときエラーが発生するのもこの場合都合が悪いので，Iferror関数で左隣のセルにデータが存在するときのみ表示されるようにしています。したがってこの例では何も表示されませんが正常な処理です。

入力できたら，同じくこれを24期の行までコピーします。

(Iferror関数 ―"Office")

見出し「期」「月」の最終行の1つ下の行に，それぞれ「25」「9月」と入力します(=「次期」を用意する)。

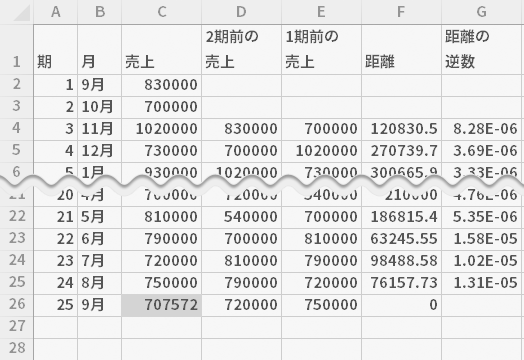
25期目の「売上」列に，「売上×ウエイト」列の上方2期を除くすべての範囲(下のシート上の緑の囲み部分)の値を合計する式を入力します。

具体的には

=SUM(J4:J25)

となります。この値を次期(25期)の予測値と見立てます。

実測値との混同を防ぐため，背景やフォントの色を変更するなどして区別をつけておいた方がいいかもしれません。あるいはコメントで注意を促してもいいかと思います。

最近隣法により次期の予測を以下の通り導きました。

表としては以上で完成です。

任意の期数に変更する

あとは採用期数をいじれば「ウエイト」列，「売上×ウエイト」列，および予測値が連動します。それぞれの項目を確認しながら採用期数をケースバイケースで変更することになります。

ここからは少しTips的なコトですが

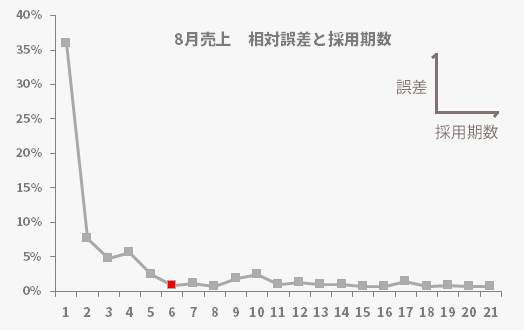
ケースバイケースとした採用期数について，ここで少し考えてみたいと思います。今回のケースでは採用期数6つで25期目の予測値を求めましたが，いまだ25期目の実測値(売上)は出ていないという想定のもとにあります。したがって実測値，予測値ともに用意できる直近のデータ，つまり第24期のデータを使って採用期数と誤差の関係を見てみたいと思います。

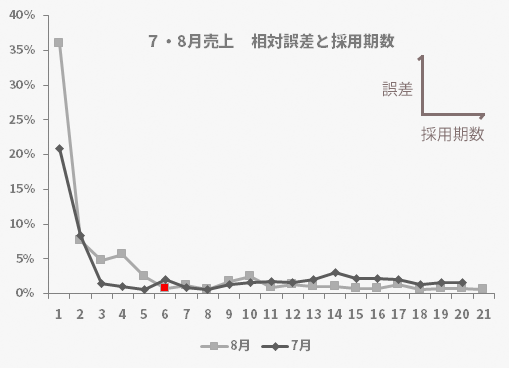
下のグラフが，その採用期数に応じた誤差をプロットしたものです。

グラフからは，今回採用した6期までにこの例における誤差の最も小さな水準にまでほぼ達していることがうかがえます。より少ない期を採用する理由はもちろんのこと，6期をこえる期をあえて採用しなければならない理由もなさそうです。その意味で，今回の所与の値とした期数「6」は，この例において妥当だと考えられる理由を1つ得たとも言えそうです。