2023/7/10
イントロダクション
ヒストグラムは,値の分布をつかむためのツールです。特定の集団・グループなどにおいて観測される値を,階級と呼ばれる区間ごとに振り分け要約して可視化します。
READ MORE
ものつくりの現場においては,ヒストグラムはQC7つ道具の1つとしてこれ以上ないほどにメジャーなツールです。ときに「誰しもが決して無縁ではいられない」といった修辞を付けても言い過ぎでないかもしれません。その有用性は事務しごとの現場でも変わることなく,たとえば金額・数量などに関する分析ツールとして利用できます。
Excelでヒストグラムを作成するとき,いくつかのアプローチを選択することができます。ただ,そのほとんどは,「度数分布表」を作成→グラフへ加工,といった大枠の流れに沿うものです。こちらでは,そのいくつかのアプローチの中から,とくに「分析ツール」と呼ばれるExcelのアドインを利用する方法をとりあげます。
またヒストグラムの書式・スタイルに関してですが,これは細部においては多様であって,分野・環境,はては作図のバックグラウンドによって定まりません。ここではQCをはじめとした工学・数学的な領域で用いられるそれではなく,一般的な事務しごとでの利用を想定した形式を成果物としたいと思います。
以下,Excelによるヒストグラムの作り方です。ここでは一連の手続きをサブスクリプション版Excel(ver.2006)で追っています。一部ボタンの配置や名称などが異なる箇所がありますが,手続きそのものは「永続ライセンス版」にいうところのExcel 2019, 2016, 2013も基本的に同じです。
なお,下のスイッチで新機能「スピル」に沿った説明に切り替えが可能です(デフォルト:OFF)。

元データ
下の表は,ある月の取扱商品の売上(万円)を個人の別に集計したものです。
こちらの会社の売上は便宜上すべて1万円単位で,それより小さな端数は生じないものとします。

成果物
2種の成果物を目的とします。
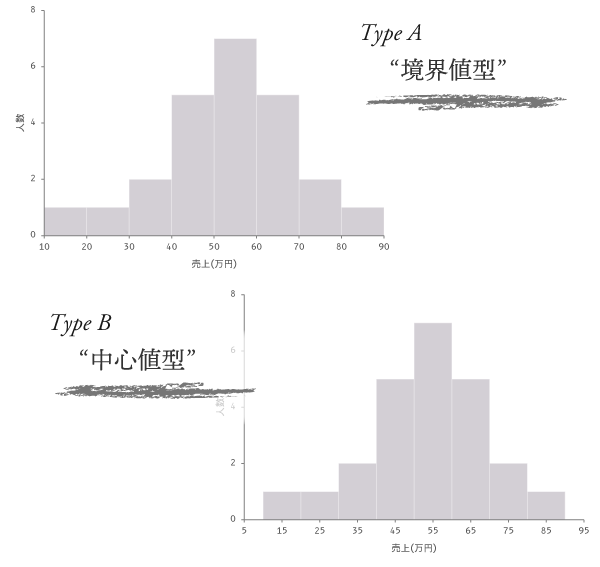
横軸の違いに注目し,ここではType Aを「境界値型」,Type Bを「中心値型」として区別します。
この場限りの用語です。
正直,この両型をExcelで描くのはちょっと面倒です。棒グラフ的な構造の作図であればそこそこ手間は減りますが,Excelではない昨今の統計処理ソフトあるいは言語を通して出力されるヒストグラムに,境界値型あるいは中心値型以外をほぼ目にすることがありません。そんな趨勢ですので,このページでも手間をペイして下の2つの型を扱っていくことにします。
バージョン2016から追加された新グラフでも未採用です(記事更新時点)。他方,GoogleのSpread Sheetでは境界値型が採用されています。
柱,階級
棒の部分を「bin(ビン)」または「柱」と呼びます。
binまたは柱と対応する横軸上の区画を「階級」と呼びます。

とりわけ,個別の階級を区別したい場合には,いちばん左の階級から順に「第1階級」,第2階級,第3階級と呼んでいくことがあります。

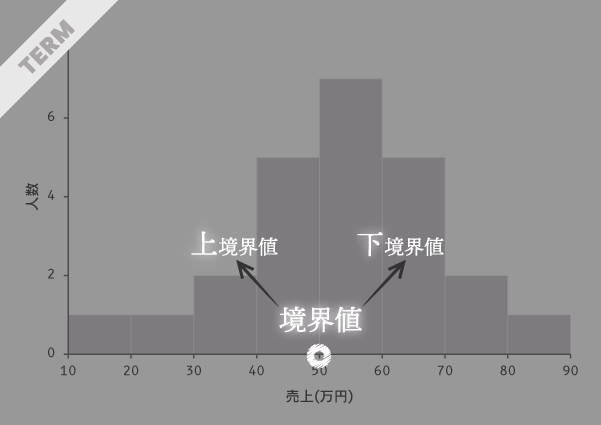
境界値
階級と階級のちょうど境目を「境界」,その値を「境界値」と呼びます。
境界値は,視点を置く階級の別にさらに区別することができます。たとえば,下の図の第4階級と第5階級の間にある境界値は,第4階級から見たときは上方側の境界値,すなわち「上境界値」であり,第5階級から見たときは下方側の境界値,すなわち「下境界値」となります。
第5階級だけに注目した場合,その下境界値は50,上境界値は60となります。
ある階級に注目したとき,上側の境界値から下側の境界値までの範囲をして「階級の幅」と呼びます。

第5階級の幅は60-50=10となります。

階級の幅は,すべての階級で等しくなるよう設計することが望まれます。
描き手にとっても整合を保つための面倒が増えますし,読み手にとっても 度数(後述)=棒の高さ といった単純明快なものさしが崩れます。とはいえ経済分野の記述統計を筆頭に不等間隔の方がハマるシチュエーションもよくあります。
さて,たとえば第5階級の中,ことばを換えれば同階級の上下境界の内で観測しうる値には,具体的にどのようなものがあるでしょうか。
1万円より小さな端数は発生しない設定なので,50, 51, 52, , 58, 59万円の10個の値

は当然として,
よくよく考えればいまひとつ,51, 52, 53, , 59, 60万円の10個の値が発生する可能性にも思い当たります。

いずれのパターンであれ,発生しうる最も値の小さいものについて「階級下限」,同・最も値の大きいものについて「階級上限」と呼ぶことがあります(この場合,数学的な上限下限とは異なります)。

ここでちょっと振り返って,上図のように2つのパターンを直覚的に区別するに至った理由を言語化してみたいと思います。
“境界上の値は,左右どっちのbinでカウントしたらよいのか,見当がつかない”
つまりヒストグラムを描くには,予めそうした不安定な要素を解消しておく必要があります。具体的には,
- 下境界値=階級下限
- 上境界値=階級上限
とする仕様から択一します。

わたしの感覚だと,えーと使い勝手といった観点だけを考えたなら,前者を選択することが多いです。また,混乱を防ぐ意味で等しく後者を適用するなど規定を設ける場合もあります。
いずれにせよ,どちらが優れるといった話ではなく,どっちをチョイスしたかを自分で把握していることが重要かと思います。便宜上このページでは,下境界値=階級下限 とする仕様のもとに話を進めます。
度数
階級の幅がすべて等しいとき,柱の高さが「度数」あるいは「頻度」を意味します。

第5階級を例とすれば,度数は7であることが読み取れます。ひらたく言えば,売上の額が50万円から59万円のいずれかである人は7人いるということです。
ヒストグラムをつくるにあたって決めること

階級の幅をいくつにするか
最初に階級の幅をいくつにするかを決めていきます。階級の幅を決めるということは,binの数を決めることと表裏です。
極論を言ってしまえば,階級の幅の選択はグラフの作成者に委ねられるべきであって,これが正解だと明言できるような解法が存在しません。
にもかかわらず,その選択こそがヒストグラムの形状を大きく左右してしまうファクターたりえるところが実に悩ましいところです。
たとえば,下のヒストグラムは10000個のランダムに生成される値の分布を1本のbinで示したものです。すぐ下のスライダーを動かして離すと,binの数を増やしたり減らしたりすることができます(IE非対応)。
さて,これら値には2つの山が隠れています。その存在を他者に強調したいとき,はたしてどのあたりの選択がbetterだといえるでしょうか。さしずめこの判断は主観に大きく依存せざるをえず,本来はそう単純に片が付くような性格のものでないことを推察できるかと思います。
そんなわけで,こうしてざっくりと眺め見た感覚とは別に,先人たちの手によって階級幅を決めるいくつかのアルゴリズムが試行錯誤されてきました。
ここでは主だったところ3つをとりあげます。
- 平方根選択
- スタージェスの公式
- スコットのルール
説明の都合3つすべてを求めますが,必須の処理という意味ではありません。もっとも判断に慣れないうちは,比較の対象がいくつかは存在した方が便利だとは思います。
平方根選択
メンバーの数(=サイズ)を$n$としたとき,平方根選択(Square-root choice)では, binの数$k$を求めてから,それをもとに階級の幅$h$を計算します。
$$k = \sqrt{n}, \qquad h = \frac{\rm{Range}}{k}$$
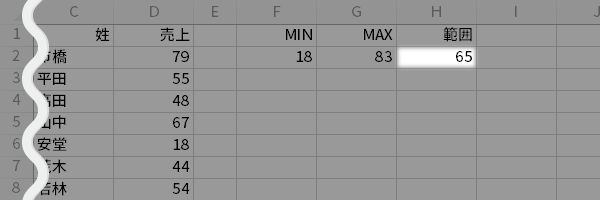
$h$を求めるのに$\rm{Range}$(範囲)が必要なので,先にMIN(最低値),MAX(最高値)を求めておき,
- CELL F2=MIN(D2:D25)
- CELL G2=MAX(D2:D25)

つづいて$\rm{Range}$を求めます。
- CELL H2=G2-F2
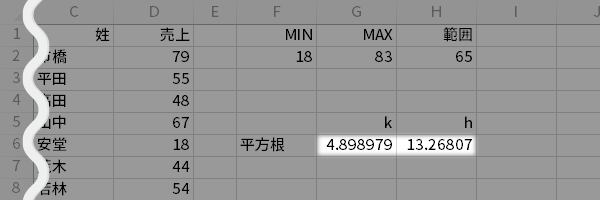
さらに$k$,$h$を次式で計算します。
- CELL G6=SQRT(COUNT(D2:D25))
- CELL H6=H2/G6
スタージェスの公式
スタージェスの公式(Sturges' formula)も同様, $k$を求めた後に$h$を導きます。
$$k = \log_2 n + 1, \qquad h = \frac{\rm{Range}}{k}$$
- CELL G7=LOG(COUNT(D2:D25), 2) + 1
- CELL H7=H2/G7
スコットのルール
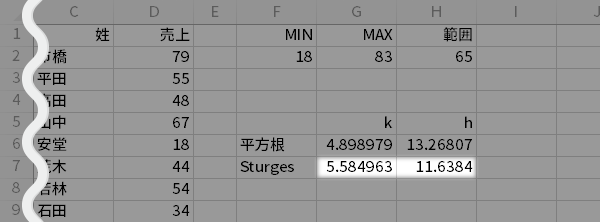
スコットのルール(Scott's normal reference rule)の場合, 直接$h$を求めにいきます。
$$h = \frac{3.5\sigma}{n^{1/3}}$$
- CELL H8=3.5 * STDEV.P(D2:D25) / COUNT(D2:D25)^(1/3)
求めた階級幅を適用する際の落とし穴
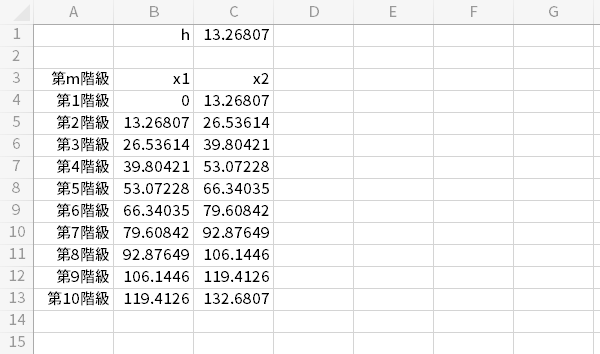
話の例えとして,仮に平方根選択の$h$,すなわち13.2681を適用する想定を置きます。
0を起点にこの$h$を幅として,とりあえず10個の階級をつくってみます。
今回ヒストグラムを通して眺めてみたいのは,売上でした。
この売上は,1万円より小さな端数が発生しないという設定です。ゆえに離散量,です。
それを踏まえたうえで,10個の階級めいめいでこの離散量がとりうる値をカウント(0を除く整数をカウントすることと同義とします)すると,結果は次のようになりました。
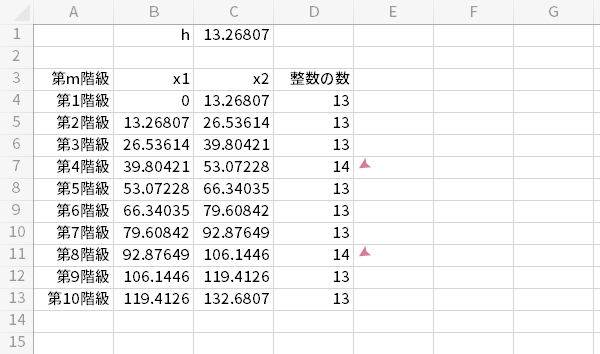
上図のとおり,等しく幅をとったにもかかわらず,カウントが揃わなかったことが分かるかと思います。これは,一般に「歯抜け」とか「くし」と呼ばれる,マズい打ち手としてやり玉に挙げられるようなヒストグラムを描いてしまう元となるので,注意が必要なところです。
求めた階級幅を丸める
こうした不都合を回避するためには,$h$を程好く丸める必要があります。補足すれば,“測定単位(最小単位)の整数倍”で丸めます。
繰り返しになりますが,この例での売上は端数が発生しない設定です。それゆえ,もしわたしの会社の売上を測定できる“秤”が手元にあったとしたならば,その最も小さなキザミは1万円を指示するに違いありません。つまり,測定単位は1万円です。
- CELL I21
他には,たとえば「0.2%単位で計れる塩分濃度計」で観測した塩分濃度であれば,測定単位は0.2といった具合になります。
少し話が逸れますが,以後の丸めの手続きも結局究極的には人,あるいは組織にそれぞれです。とはいえ,そのひとことで片付けてしまっては,ここで説明をはじめてしまった身としてもどうかとは思うので,わたし自身の“丸め方”を具体例として挙げていきます。
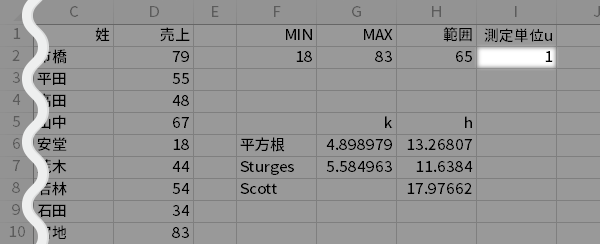
ということで,残る「整数倍」という表現ですがなんだか際限なさそうな感じでどこか不安を覚えます。しかし幸い,「慣例的に」と言うべきか,掛け算の相手としては 1,2,5,10 の4つの値だけをキーナンバーライクにとらえておけば,多様な元データを相手にしても応用が利くことが多いです。したがって下図のように,求めた$h$の右方にでも先に挙げた4つの値,すなわち 1,2,5,10 を置いておきます。

そして,測定単位をこれら整数と掛け合わせます
- CELL I5=\$I\$2 * I4
- CELL I5=I2 * I4:L4

つづいて,$h$の常用対数を10の指数として先の値とを掛け合わせてみると,下図のような値が求められます。
- CELL I6=I\$5 * POWER(10, INT(LOG10(\$H6)))
- CELL I6=I5# * POWER(10, INT(LOG10(H6:H8)))
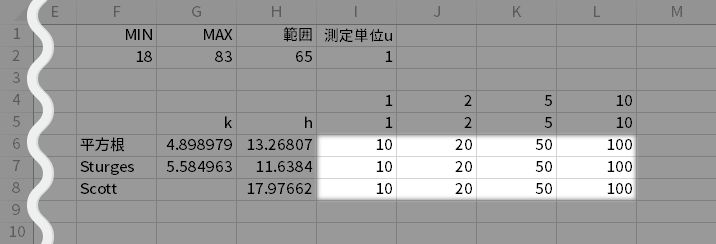
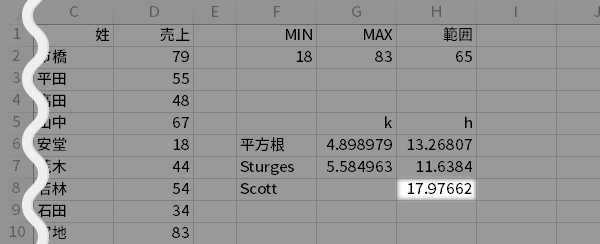
各アルゴリズムの丸めていない$h$ (上図の「h」列)と,その右に並ぶ同じ行の数字を照らして,近そうな値を探します。たとえば平方根・スタージェスを採用した場合は10,スコットを採用した場合は20あたりが丸めとしては適当かなと見積もることができます。
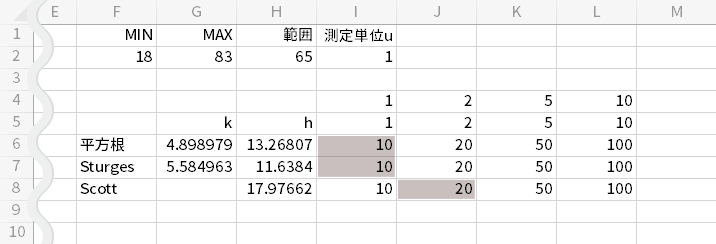
このとき,範囲が65なので,$h=10$を選択した場合はbinの数にして$6+\alpha$本,$h=20$を選択した場合は同じく$3+\alpha$本程度のヒストグラムとなることが予期できます。
キーナンバー「1, 2, 5, 10」でよい値が見つからなかった場合(測定単位がより小さいか,より大きい場合),20, 50, 100, あるいは , 0.1, 0.2, 0.5 といった感じにオリジナルのキーナンバーを$10^d$倍しながら前後にスコープを拡げ,探索を繰り返します($d$: 0を初期値と考えてインクリメント,あるいはデクリメント)。と言っても慣れれば億劫な作業なので,測定単位から$d$の見当を直接つけてもよいでしょう。その場合,キーナンバーを配列数式,またはスピルで CELL I4:L4 ={1,2,5,10}*POWER(10, -INT(LOG10(I2))) と置き換えます。
$6+\alpha$本と$3+\alpha$本のどちらかを選べと言われれば,後者はやっぱりいくらかbinが少ないような感じだし,分布を表現するには若干心もとないかもといった考えがよぎるので,この例では前者を選択することに決めたいと思います。
つまりこの売上の事例では,平方根あるいはスタージェスを利用します。とはいえどっちを使うか明言しないと以降の計算に秩序がなくなるので,シート上の計算ではセルI16の平方根の結果の方を使います。
第1階級の下境界値を決める
さて,次のステップでは第1階級をいくつからとり始めるかについてを決める必要があります。下の境界値型の図で言えば,横軸の左端,赤く強調した目盛をいくつにするかを決めること,です。
先に見たように,この部分は第1階級の下境界値で,値そのものはラベルから10であることが読み取れます。
言ってみれば大げさに構える必要性も感じない,何の変哲もない存在にしか思えません。
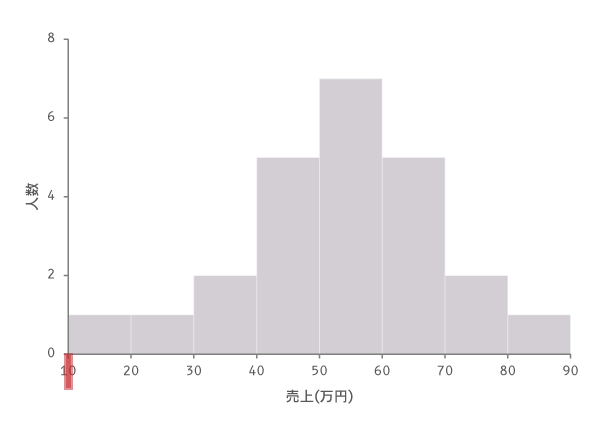
重ね重ねの難点列挙になりますが,第1階級の下境界もヒストグラムの形状を大きく左右してしまうファクターであることは,実のところあまり目立たないのが厄介です。
参考までに下に4つの境界値をテストしてみた結果を示します。階級の幅は変えずに下境界を少しずらしただけでも,ヒストグラムの印象がずいぶん変わるのが分かるかと思います。$n$が小さければ,尚更です。
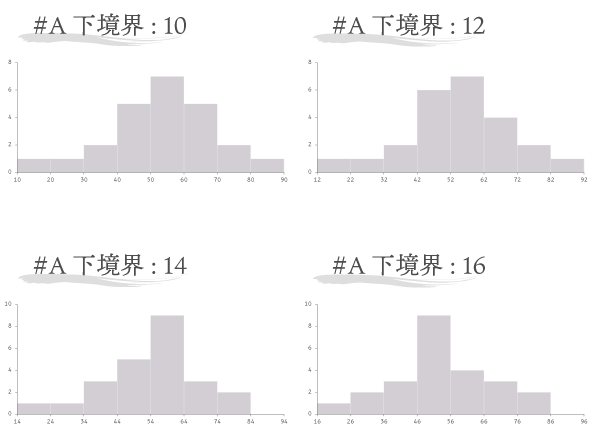
これまでのファクターと同様,正解が存在する類の設定ではないので悩ましいこと然りです。が,基本的には任意のbinとbinの間に平均値をもっていきたいといったような明確な意図がない場合や,QCのような精緻な観測工程以外の一般的なビジネス実務の場面では,ラベルの読みやすさをキープする方向(境界値がなるべくキリのいい値で納まるように:14, 24, よりも 10, 20, のが,他者が読んでもピンとくる!)で決めていくのが妥当なように,わたし的には感じます。
それゆえ,
- CELL F11=FLOOR.MATH(F2, I6)
でMINより低く,かつ最も近い$h$の倍数を探し出し,これを第1階級の下境界(階級下限)として用います。
階級を定義する(分析ツール前の準備)
ヒストグラムの階級すべてをフォローしていきます。
まず,見出し
- 階級名
- 下境界
- 上境界
- 上境界-u/2
を用意します。
1番目の階級であることを入力し,さらには下境界値,上境界値を求めます。
- CELL F14第1階級
- CELL G14=IF(COUNTA(\$F\$14:F14)=1,\$F\$11,H13)
- CELL H14=G14+\$I\$6
下境界値,上境界値を求めます。上境界値がMAXを超えるまで階級をつくればよいので,その数を計算しつつ必要なだけ下境界値を用意してから,
- CELL G14=IF(((G2-F11)/I6)-QUOTIENT(G2-F11,I6)<>0, SEQUENCE(ROUNDUP((G2-F11)/I6,0), 1, F11, I6), SEQUENCE(ROUNDUP((G2-F11)/I6,0)+1, 1, F11, I6))
それぞれに対応する上境界値もつくります。
- CELL H14=G14#+I6
そのうえで,用意した各階級に対し名前を振っていきます。
- CELL F14="第" & SEQUENCE(ROUNDUP((G2-F11)/I6,0), 1) & "階級"
つづいて4後段で決めた,境界上の値を処理するルールを適用するため,上境界値より測定単位の1/2倍だけ小さな値をつくります。別のことばを使えば,階級上限と上境界値のちょうど真ん中を,度数を求める上での閾とします。
- CELL I14=H14-\$I\$2/2
- CELL I14=H14#-I2/2
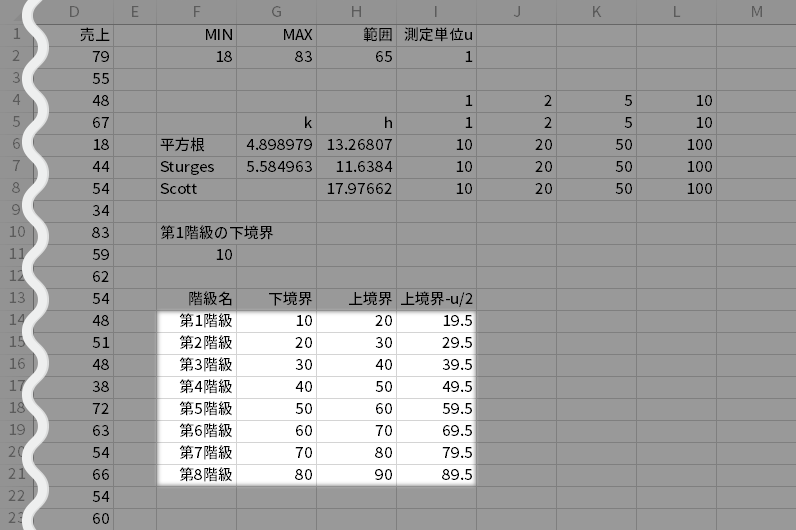
というのも後述の分析ツールは,“ある値以下”の条件でカウントを実行するからです。この場合の「ある値」として利用するのが,境界上の値を含まない「上境界-u/2」列ということです。
とにもかくにも,用意したセル範囲F14:I14を,「上境界」でMAXがカバーできるところまで下方へとコピーします(最後の階級の上境界値>MAX)。
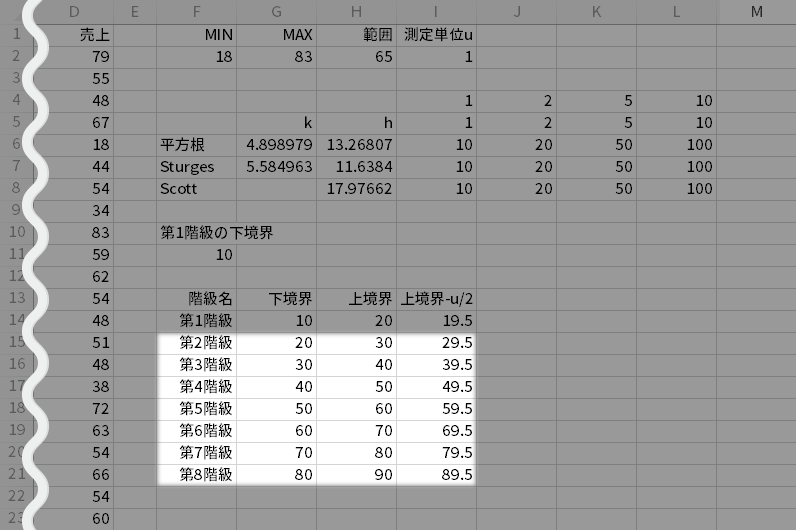
なお最後の階級の直前で 上境界値=MAX が成立した場合,ユーザーの判断でこの階級の「上境界-u/2」だけ上境界値と同じ値に書き換えて,最後の階級と統合を図ることがあります。
100点満点のテストの得点分布を10本のbinで見る場合が好例。
分析ツールを走らせる
データタブ分析グループのデータ分析ボタンをクリックします。
ボタンが表示されていない場合,「分析ツール」アドインのインストールが必要です(分析ツールを読み込む ―"Office")。
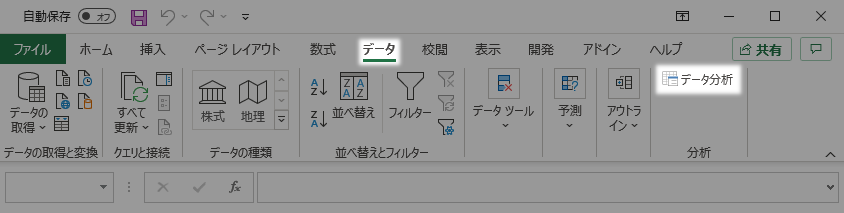
データ分析ダイアログが開いたらヒストグラムを選択してOKボタンをクリックします。
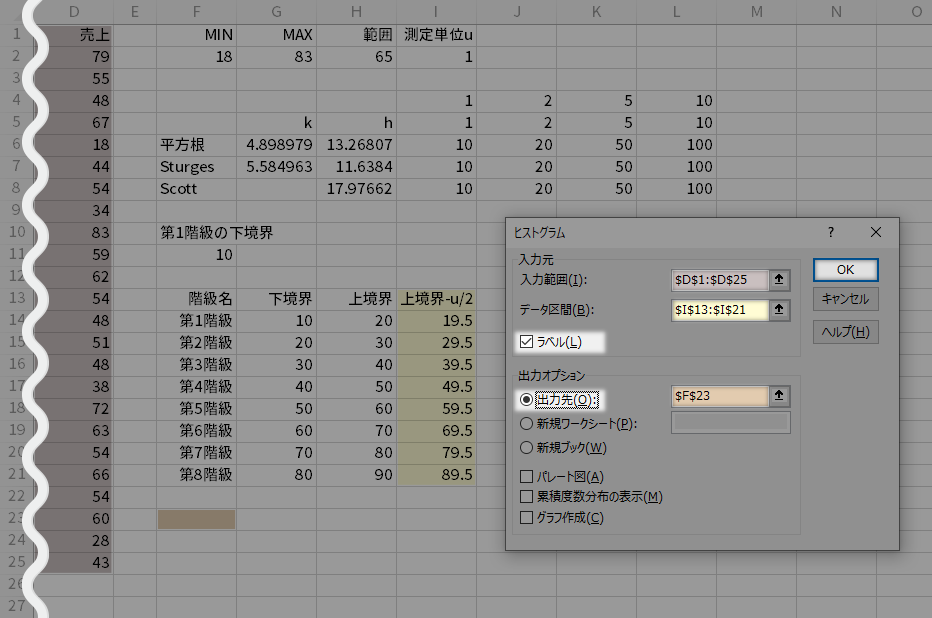
ヒストグラムダイアログの入力範囲とデータ区間,および出力先を,下図の対応のようにそれぞれ指定します。
ここでは見出しも選択していますので,ラベルのチェックも必要です。
一連の指示を済ませたら,OKボタンを返します。
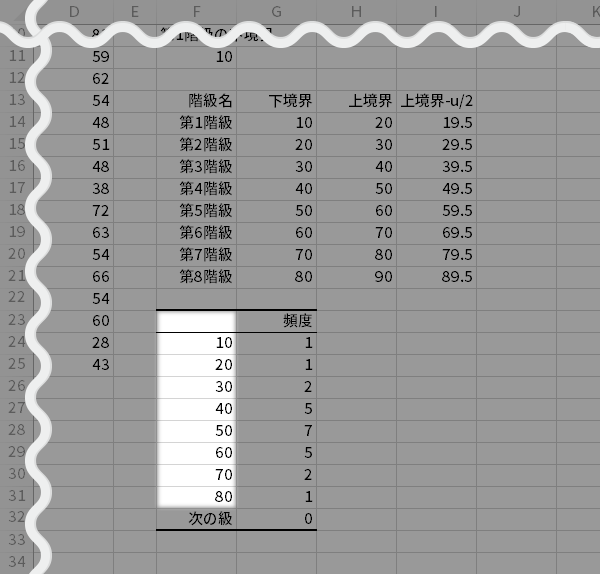
「度数分布表」を手に入れることができました。
埒外なので仔細には触れませんが,度数分布表自体が目的である場合は,左の列を階級として上下限や境界値で紡ぐなど読み手にとって理解しやすいものに加工する必要があります。
いずれにせよ,目的のヒストグラムはこの表をソースとして描いていきます。

もっともヒストグラムを目的とした場合でも,工程数を減らす工夫は惜しむべきではないでしょう。それゆえ見出し部分を消去したうえ直下の内容を「下境界」列と同じ値で上書きし,いうなれば(グラフ化という)目的のためにExcelが解析しやすい構造をつくっておきます。
- CELL F23(削除)
- CELL F24=G14
もっともヒストグラムを目的とした場合でも,工程数を減らす工夫は惜しむべきではないでしょう。それゆえ見出しとその直下から始まる値のすべてを消去したうえセルF24から下方に向かって「下境界」列と同じ値を転記していきます。いうなれば(グラフ化という)目的のためにExcelが解析しやすい構造をつくります。
- CELL F23:F31(削除)
- CELL F24=G14#
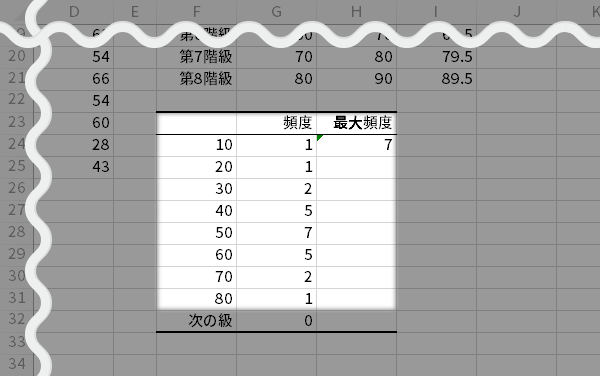
「最大頻度」を計算します。これも直前の手と同様の趣旨からです。
- CELL H23最大頻度
- CELL H24=MAX(G24:G31)

棒グラフと散布図を素地とするヒストグラム|境界値型
境界値型のヒストグラムを描いていきます。なお中心値型も一度この過程を経ることが必須です。
「次の級」を除く見出しを含めた度数分布表を選択し,
挿入タブグラフグループの縦棒/横棒グラフの挿入ボタンをクリックします。
プルダウンから集合縦棒を選びます。

これにより,シートの上に棒グラフが挿入されます。
グラフが選択された状態より,書式タブ現在の選択範囲グループから,選択対象を頻度系列に切り替えて,直下の選択対象の書式設定ボタンをクリックします。
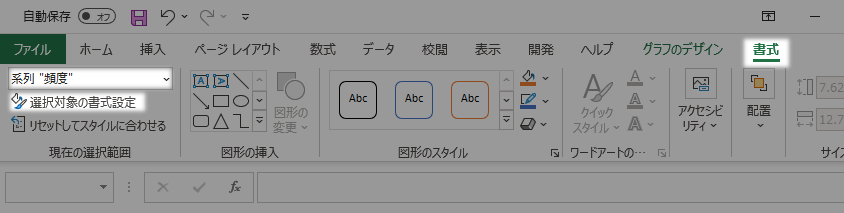
データ系列の書式設定ウインドウの要素の間隔を,0%に設定し,使用する軸を第2軸に切り替えます。
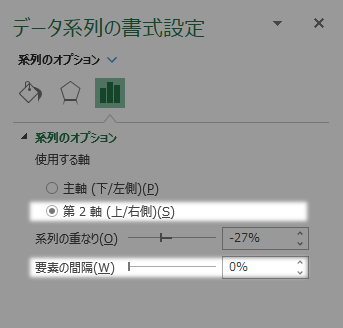
グラフのデザインタブ種類グループのグラフの種類の変更ボタンをクリックします。
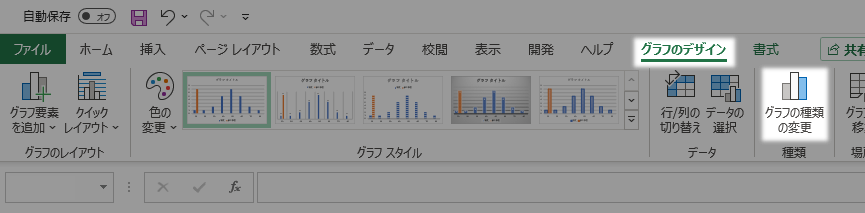
グラフの種類の変更ダイアログが開きます。最大頻度系列を直線(散布図)に変更してOKを返します。
22でしたのと同様に,今度は横(値)軸の書式設定ウインドウを呼び出します。
最小値最大値および主の各値を設定します。具体的には,
- 最小値:第1階級の下境界値
- 最大値:最後の階級(第8階級)の上境界値
- 主:$h$の整数(基本的には1)倍。
を各値とします。
そして境界値型では目盛線も不可欠でしょう(目盛の種類外向きなど)。
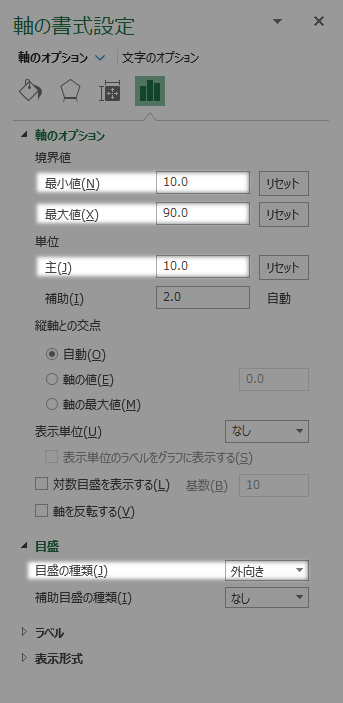
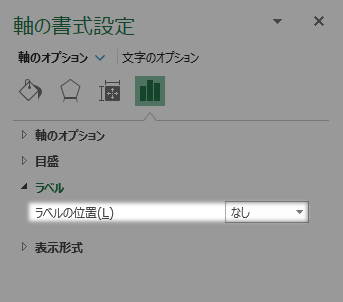
最後に第2縦軸を不可視にします。これはラベルの位置をなしに変えて実現します。
境界値型ヒストグラムの完成です。

なお,プレゼンなどの場で評価者と対峙すると「たとえば20ってどの棒に入るの?」なんて不意打ちが飛んできたりすることがあります。概ね発表者の見識を見定めるための意地悪なんて言うのは冗談ですが,とはいえそうした基本的な仕様にあまりに無関心すぎると,不幸にも「ただ漫然とツールを通してきただけ」判定をくらったりもしてしまうので,侮れないところがあります。
中心値型に転化する,追加の工程
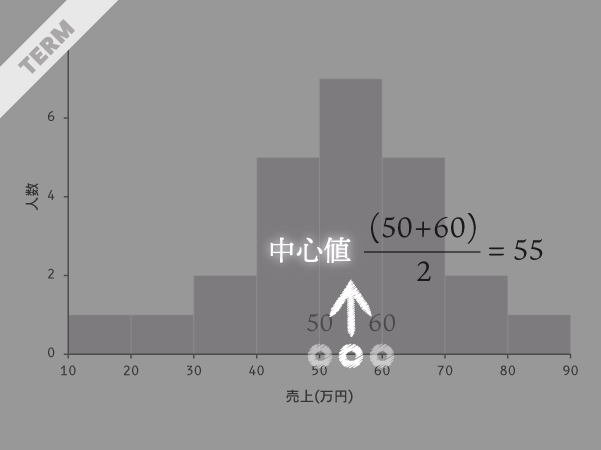
「中心値」は階級を代表する値:階級値のひとつとして利用されます。
ある階級の下境界と上境界の真ん中の値を指し,第5階級で例えれば,中心値は(50+60)/2=55と求められます。
以下,横軸をこれに転換するための工程です。
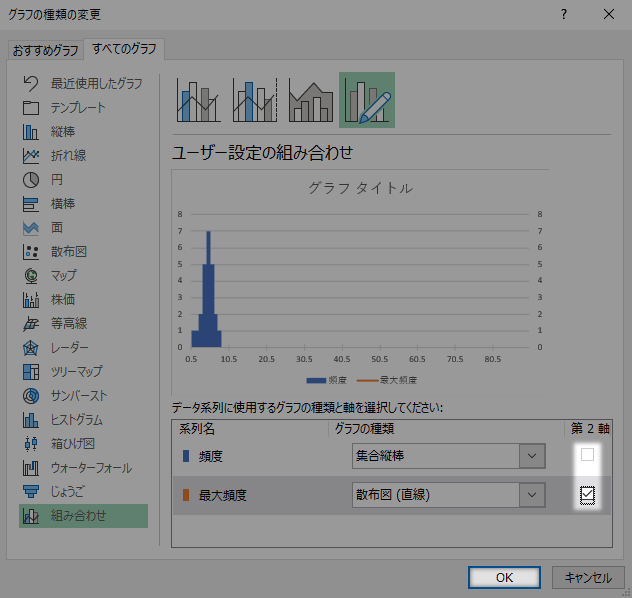
グラフの種類の変更ダイアログから頻度系列と最大頻度系列の第2軸を入れ替えます。
中央値型では最大頻度系列側を第2軸に設定します。
グラフのデザインタブグラフのレイアウトグループのグラフの要素の追加ボタンをクリックします。
プルダウンを軸第2横軸とたどっていきます。
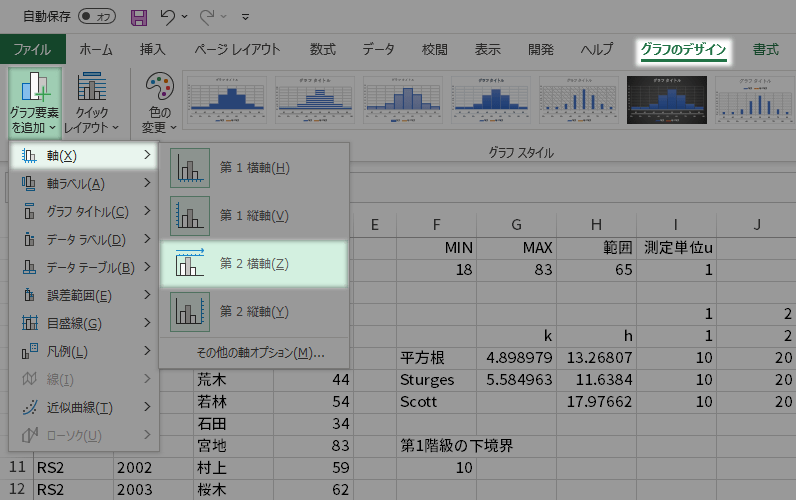
第2軸 横(値)軸の書式設定ウインドウを呼び出します。
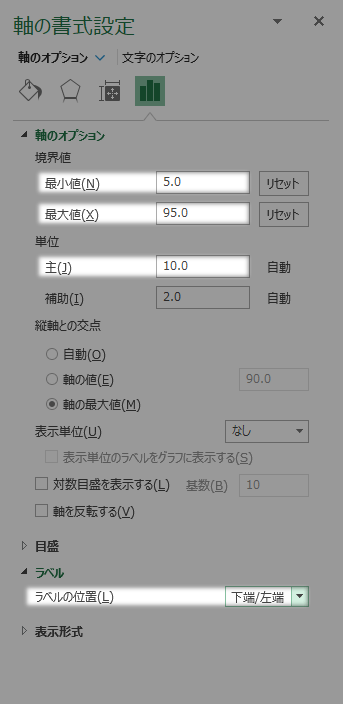
最小値最大値および主の各値を設定します。具体的には,
- 最小値:第1階級の下境界値$-h/2$
- 最大値:最後の階級(第8階級)の上境界値$+h/2$
- 主:$h$の整数(基本的には1)倍。
を各値とします。
そしてラベルの位置を下端/左端に動かします。
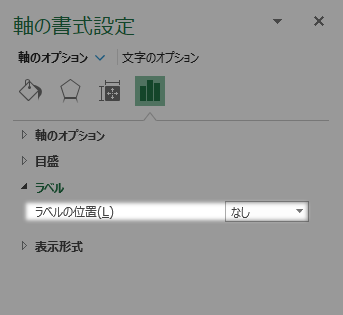
他方,横(値)軸について,ラベルの位置をなしとして不可視にします。
中心値型の完成です。







