2023/7/10
イントロダクション
産業連関表(I-O表,投入産出表とも)は,国・県など一定の地域で,一定の期間においておこなわれた財やサービスの取引額を表としてまとめたものです。日本では原則として5年ごとに作成され,最終需要の変化に応じた生産・雇用への波及効果の計算から,価格上昇がもたらす他産業への影響度の計算,ひいては環境問題への応用に至るまで,さまざまな目的で利用されています。
READ MORE
産業連関表のタテ(列)方向は,特定の部門が財・サービスの生産にあたって投入した中間財(原材料)ないし付加価値の額を,ヨコ(行)方向は,特定の部門が生産した財・サービスが中間財または最終財として需要された額を示しています。言い換えれば,前者は費用の構成,後者は販売の構成といったところを意味しています。

ここでは,分析上の必要に応じて,公表された産業連関表の部門を任意に集約するといった趣旨のもとで,x部門の産業連関表をy部門のそれに変換する作業(x>y),ならびに,生産波及効果を計るために必要な投入係数表・逆行列係数表を作成する手順を追っていきます。ただし,このサイトには産業連関表に関する複雑かつ精緻な領域にまで踏み込める見識はありません。したがって,このプロセスは産業連関分析の中でもきわめて基本的な部分にすぎないことをご留意ください。
以下,Excel 2016 を使った産業連関表の部門統合のすすめ方と,投入係数表・逆行列係数表の作り方です。一部ボタンの配置や名称などが異なる箇所がありますが(この場合,可能であれば当該箇所に明記します),手続きそのものは,「永続ライセンス版」にいうところの Excel 2019, Excel 2013 あるいは Excel 2010,そして,「Office365版」の Excel (本頁更新時点のver.1905)でも基本的には同じです。

元データ
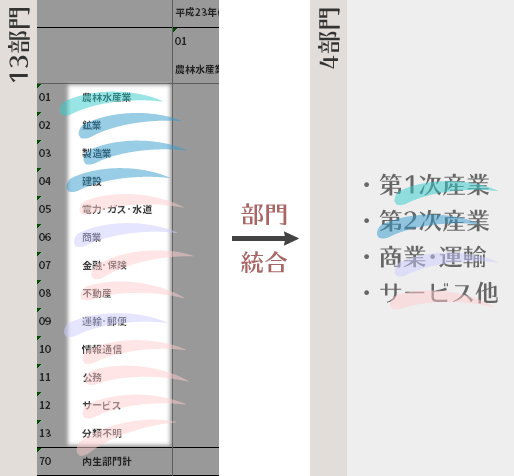
元のデータです。e-Statで公表されている平成23(2011)年の日本の産業連関表(取引基本表・生産者価格評価表・13部門分類)です。
このシートの名前(シート名)は,「元表」とする前提で進めます。ここでは,この元表から4部門の統合表を作成し,それをもとに投入係数表と逆行列係数表を作成することを目的とします。
部門統合
元表の産業連関表(取引基本表・生産者価格評価表・13部門表)は,下のように「農林水産業」から「分類不明」まで13の部門に分かれています。13部門表は上述のウェブページに掲示の産業連関表の中でも最も部門数の少ないものですが,ここではさらに集約して,
- 第1次産業
- 第2次産業
- 商業・運輸
- サービス他
の4つの部門からなる産業連関表を作成していきたいと思います。このようにして適宜部門を統合する作業は,部門統合 と呼ばれます。

具体的には,下のように統合したいと考えます。
第1次産業からサービス他まで,それぞれ対応する色の部門を1つにまとめてしまいます。
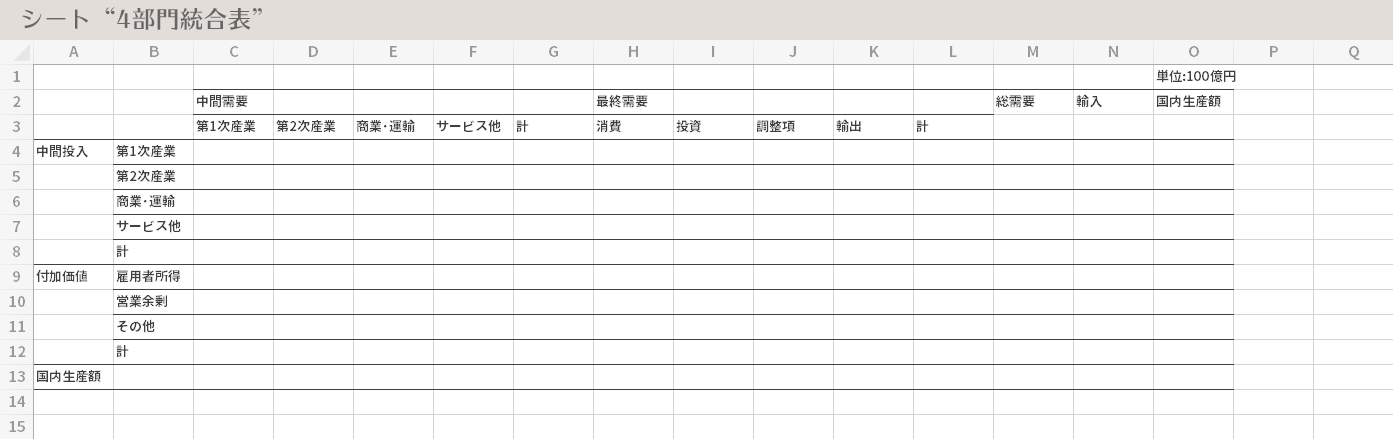
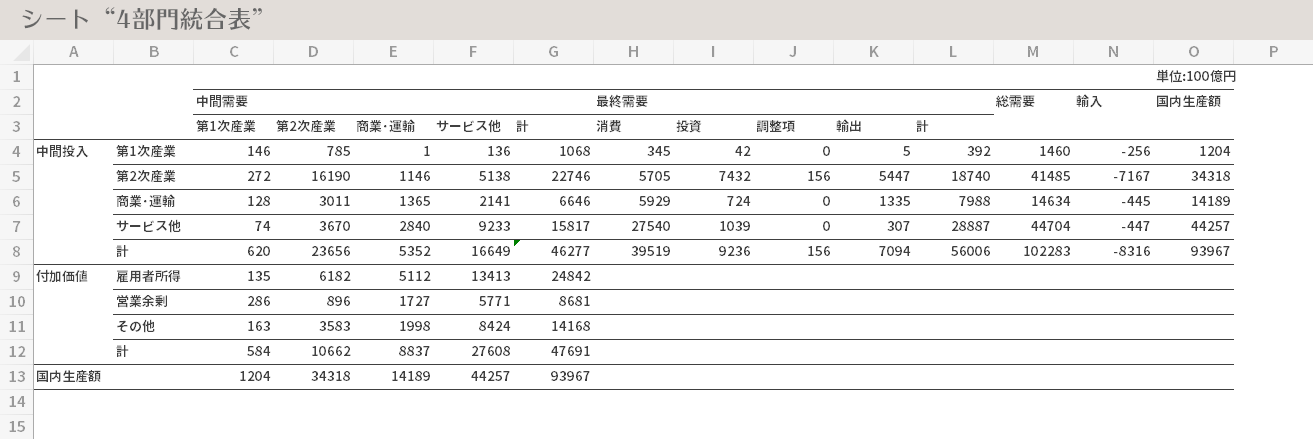
それでは別のシートを用意し(シート名: 4部門統合表),下のような表の枠組みを作成しておきます。
入力が面倒な場合は リンク をクリックであたらしいタブに表組みを開き,それをシート「4部門統合表」のセルA1にコピーしてもかまいません。
では,ここから部門統合の作業へと入ります。しばらくはそのための準備作業がつづきます。
最初にシート「元表」に切り替えて,3行目,およびB列にそれぞれ行と列を挿入しておきます。
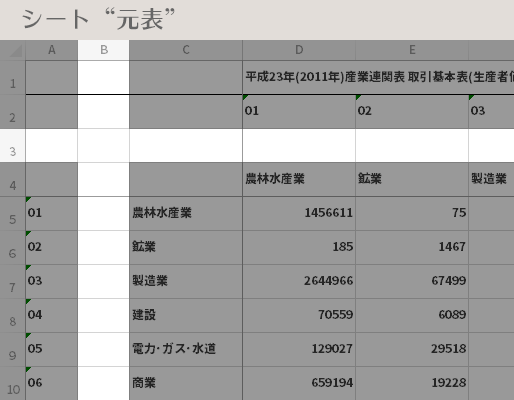
挿入した行および列に,下のように識別番号としての役割を与えた数字を割り振ります。
具体的には,最初は下図のハイライトの領域を処理しますが,これは先に決めたルールにしたがって,
- 第1次産業 … ' 1 '
- 第2次産業 … ' 2 '
- 商業・運輸 … ' 3 '
- サービス他 … ' 4 '
と各番号を充てていきたいと思います。
数字の割り振りが終わったら,同じくハイライトの領域をクリップボードにコピーして
![[識別番号]第1次産業…1,第2次産業…2,商業・運輸…3,サービス他…4](../images/howto/io-table/step6.png)
列見出し「農林水産業」の真上のセル(ここではセルD3)に,行列を入れ替えて貼り付けます。
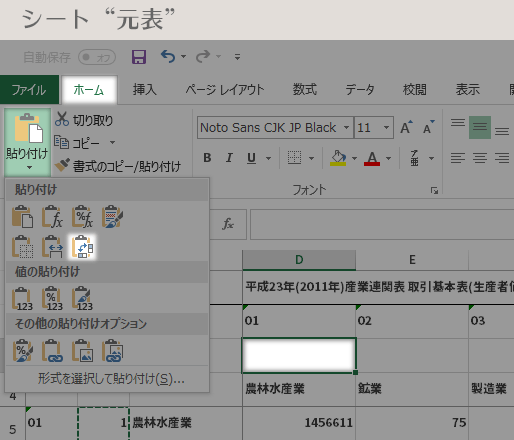
念のため,上の操作で列見出し「分類不明」(ここではP列)まで識別番号がきちんとコピーされていることを確認しておきます。
さて,ここまでの作業で,下の図のグレーで塗りつぶしたエリア(内生部門)に関しての準備を終えたことになります。
ここから,その直右のエリア(最終需要部門)を処理していきます。

次のエリアを処理するにあたっては,下の図のようにおこないたいと思います。
具体的には,「家計外消費支出」「民間消費支出」「一般政府消費支出」を消費として,「国内総固定資本形成」「在庫純増」を投資として,「調整項」を調整項として,「輸出計」を輸出として,そして「輸入計」を輸入とし,順に11・12・13・14・15の識別番号を割り当てます。
- 消費 … ' 11 '
- 投資 … ' 12 '
- 調整項 … ' 13 '
- 輸出計 … ' 14 '
- 輸入計 … ' 15 '
この番号を,各列見出しの真下のセルに入力します。
![[最終需要部門の識別番号]消費…11,投資…12,調整項…13,輸出…14,輸入…15](../images/howto/io-table/step9.png)
この時点で,下の図のグレーのエリアに関する準備を終えました。
ここから残る1枠(付加価値部門)に手をつけます。

次のエリアを処理するにあたっては,下の図のようにおこないたいと思います。
具体的には,「雇用者所得」を雇用者所得として,「営業余剰」を営業余剰として,「家計外消費支出」「資本減耗引当」「間接税(除関税)」「経常補助金」をその他とし,順に21・22・23の識別番号を割り当てます。
- 雇用者所得 … ' 21 '
- 営業余剰 … ' 22 '
- その他 … ' 23 '
この番号を,各行見出しの左隣のセルに入力します。
![[付加価値部門の識別番号]雇用者所得…21,営業余剰…22,その他…23](../images/howto/io-table/step11.png)
ここまでの作業で,3か所すべて(内生部門と最終需要部門および付加価値部門。なお,後の二者は総称して外生部門と呼ばれます)の準備を終えました。
ここからは,先の手順で割り振った番号をキーにデータの集計をおこないます。

では早速,「4部門統合表」に切り替えます。
まず,表下の使用していない任意のセルをアクティブにしておきます(ここではセルB16)。このセルを基点に集計した値を出力していくことになります。
次に,リボンのデータタブデータツールグループにある統合ボタンをクリックすると
![[4部門統合表]セルB17をアクティブ→データ→統合](../images/howto/io-table/step13.png)
統合の設定ダイアログが表示されます。
統合元範囲のテキストボックスをアクティブにして,「元表」に切り替えます。
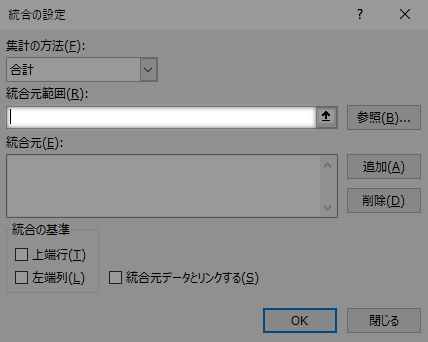
識別番号が入力された行・列の交点を基点として(ここではセルB3),同じく識別番号が入力された最右方(ここではAF列)の列および最下方の行(ここでは24行)の交点(つまりセルAF24)までを選択します。
![[元表]セル範囲B3:AF24を選択](../images/howto/io-table/step15.png)
統合の基準の上端行,左端列ともにチェックを入れ,OKボタンを返します。
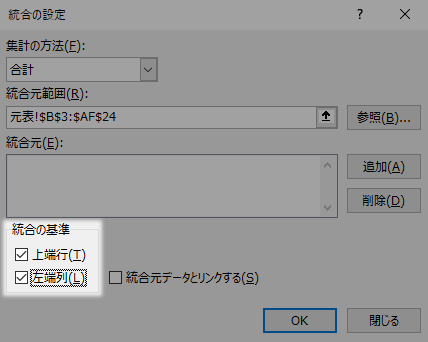
以上の作業で,値が集計され「4部門統合表」に出力されたかと思います(下図)。
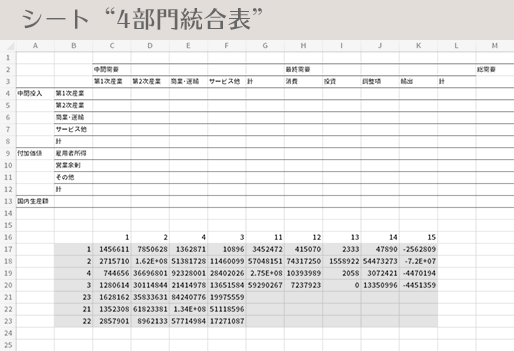
ただし,現状の集計結果は行列ともに識別番号の順に並んでいない箇所があることがわかります。これを上の表の並びと対応させるため,並べ替えをおこないたいと思います。
では,まずは行方向の並べ替えをおこなうとして,
下図・上段の図のグレーの矩形部分を選択し
リボンのデータタブ並べ替えとフィルターグループにある並べ替えボタンをクリックして(下図・中段)
並べ替えダイアログの設定を下図・下段のように設定してOKボタンを返します。
![[4部門統合表]タテの並べ替え](../images/howto/io-table/step17-3.png)
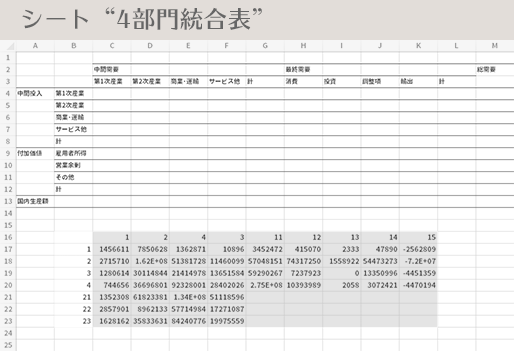
つづいては列方向の並べ替えです。
下図・1段目の図のグレーの矩形部分を選択し
先と同様ダイアログを呼び出して,オプションボタンをクリックします(下図・2段目)。
方向を列単位に変え(下図・3段目)
並べ替えダイアログの設定を下図・4段目の図のように設定してOKボタンを返します。
![[4部門統合表]ヨコの並べ替え](../images/howto/io-table/step18-4.png)
ここらで4部門統合表の右肩に記載の単位(100億円)と,集計値の単位(「元表」の単位: “100万円”)とを合わせておきたいと思います。
ただしこの修正は,これまでの過程で作成した集計表に直接加えるものとします。
具体的にはこの場合,集計値を10000で除算すれば単位がそろうことがわかります。したがってシートの上の任意の場所に10000を一時的に入力し,これをクリップボードにコピーしておきます(下図・1段目)。
そして下図・2段目の領域を選択し
リボンのホームタブクリップボードグループにある貼り付けボタンのプルダウンから形式を選択して貼り付けを選びます(下図・3段目)。
形式を選択して貼り付けダイアログの設定を下図・4段目の図のように設定してOKボタンを返します。
以上の操作により,集計値に直接の除算を実行することができます。なお最初に入力した10000については,残しておくと何らのミスを誘発することもあるかもしれません。したがって,この時点でシートから削除しておいたほうがbetterかと思います。

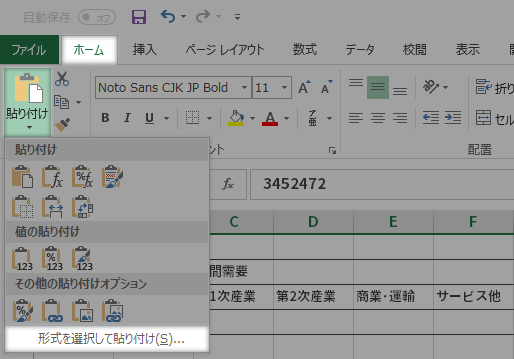
集計値と,そもそもの4部門統合表の列見出し・行見出しの位置関係とが合致するよう,集計値の特定の領域を適宜移動させることで調整します(下図・上段)。
調整後,下図・下段の図のグレーの矩形部分をクリップボードにコピーします。
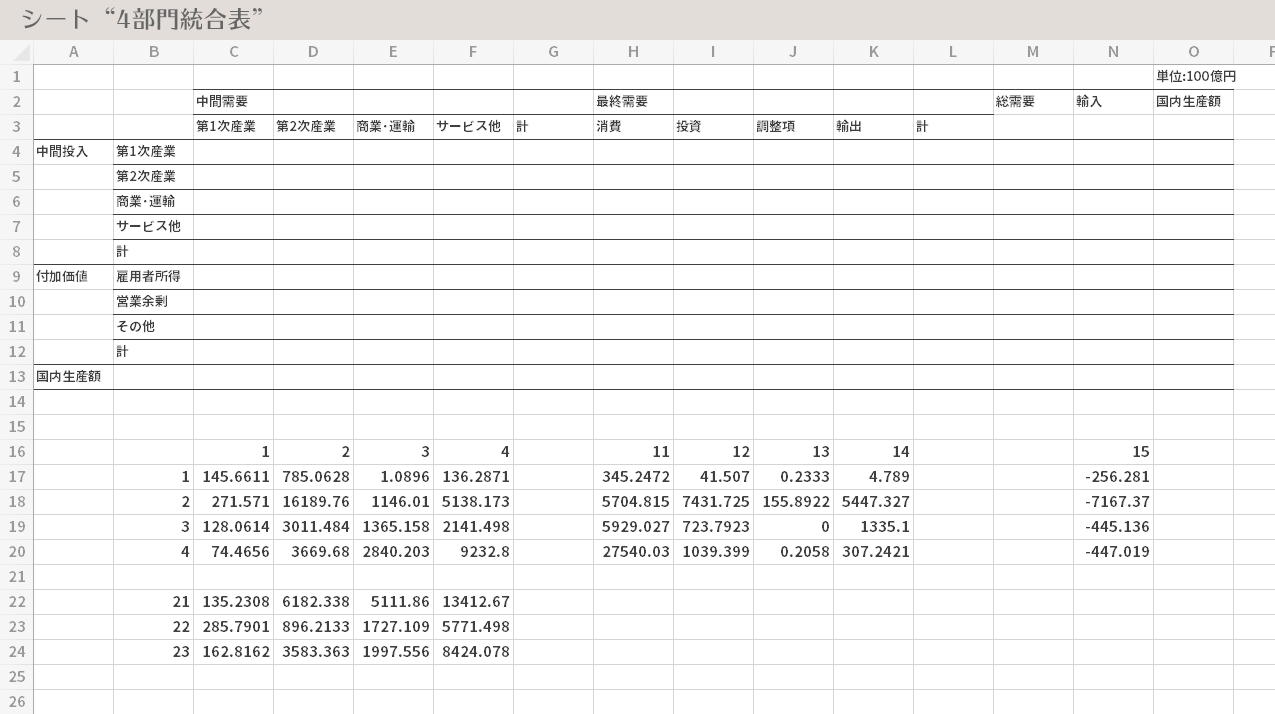
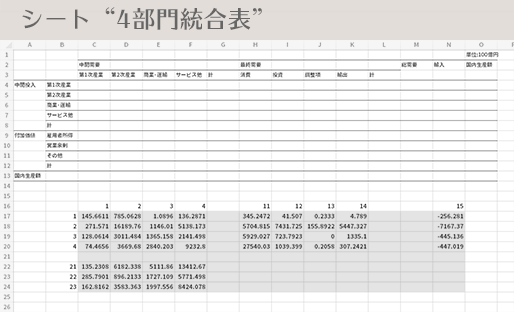
クリップボードの内容を,セルC4にペーストします。
その後,下図の色の異なる4つの領域について,選択オートサムボタンで行計および列計をエリアごとに求めていきます。
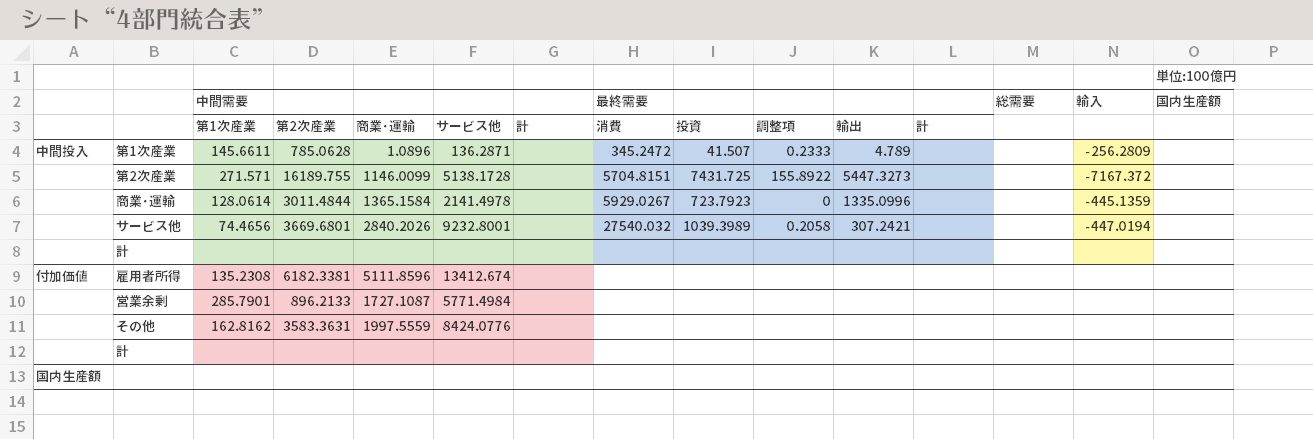
残る「総需要」「国内生産額」の各セル(下図のうち,パープルで彩色した領域)を計算し埋めていきます。
計算式は次のとおりです。
- M列の「総需要」中間需要の「計」+ 最終需要の「計」
- O列の「国内生産額」「総需要」+「輸入」(つまり輸入が控除されます)
- 13行の「国内生産額」中間投入の「計」+ 付加価値の「計」
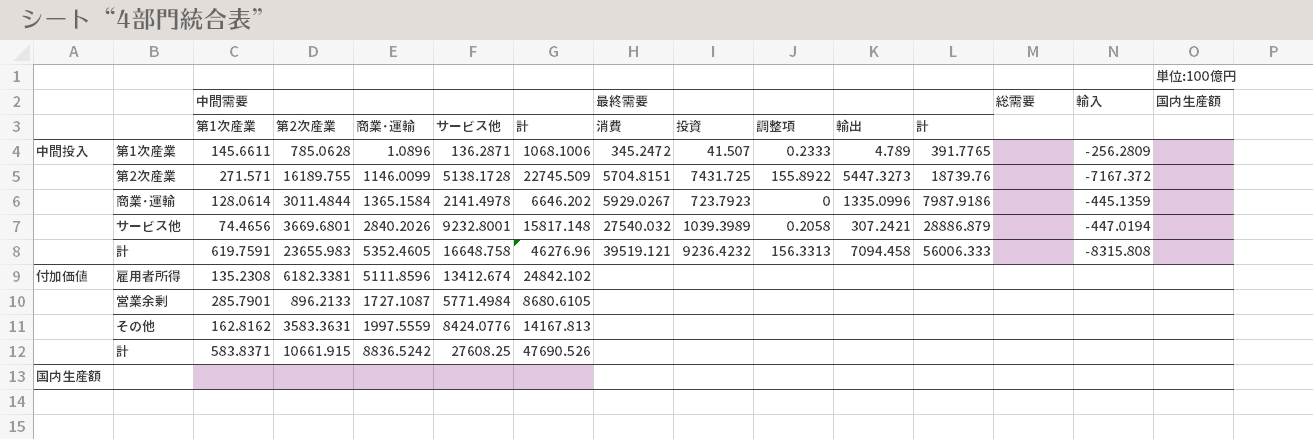
「4部門統合表」の完成です。
この表を作成するために使用した集計値に関しては,整合を確認した後であれば,この時点で削除してもかまいません。
構成比を求めてみる
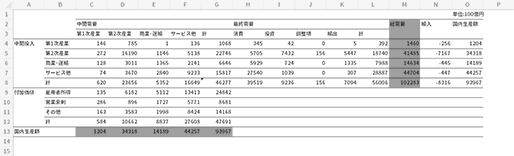
何をなせるかの参考として,ここで4部門統合表をもとに,産業構造をちら見しておきたいと思います。たとえば下図・1段目の図のグレーの項目具体的には行方向の「国内生産額」,列方向の「総需要」を1(100%)とした場合,
前者の構造は下図・2段目のように,後者の構造は下図・3段目の図のように可視化することができます(帯グラフ)。
また行・列のいずれをも同時に可視化の対象に含めたい場合には,マリメッコチャート(モザイク図)が便利です。たとえばこのマリメッコチャートを使って最終需要と産業とをクロスさせてみると,下図・4段目の図のような構造を示すことができます(姉妹サイト「BDAstyle」のジェネレータサービス“マリメッコチャートジェネレータ on Web”で作成。ただしコードの一部について,調整のため手を加えてあります)。
またここでの4部門表においては適したケースとはなりませんが,中間投入,および中間需要の割合を産業別に散布図にプロットして産業の相互依存関係を見るようなアプローチも場合によっては考えられます(下図・5段目,cf. [PDF]産業連関表による平成23年神戸市経済の概要 ―"神戸市", p.12.)。
いずれにしろ,こうした視点については行政が公表するあまたの文書に示唆が豊富であることを加えておきます。




投入係数表
さて,ここからは投入係数および付加価値率を求めます。これを表としてかたちにしたものを投入係数表と呼びます。
投入係数は,ある1単位の商品を製造するのに必要となる商品(=原材料)の投入量を意味します。また,付加価値率はある1単位の商品を製造するのに必要となる労働あるいは資本の投入量を意味しています。
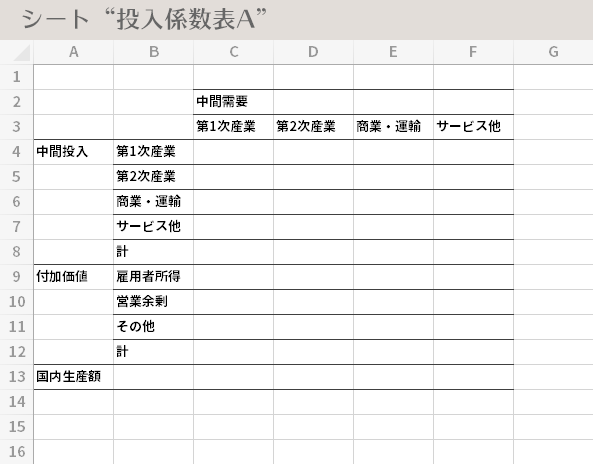
それでは別のシートを用意し(シート名: 投入係数表A),下のような表の枠組みを作成しておきます。
こちらも入力が面倒な場合は リンク をクリックであたらしいタブに表組みを開き,それをシート「投入係数表A」のセルA1にコピーしてもOKです。
「第1次産業」の交点のセル(ここではセルC4)に,
(4部門統合表の)第1次産業の中間投入額÷国内生産額
となる計算式を入力します。
- ='4部門統合表'!C4/'4部門統合表'!C$13
この式を表の最右列までヨコにコピーしたのち,そのまま表の最下行までタテにコピーします。

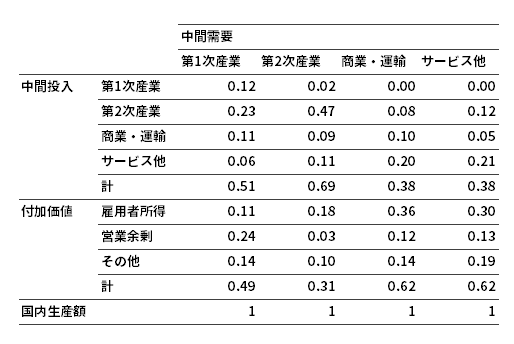
投入係数表の完成です。
ここで“ある1単位の商品を製造するのに必要となる”という観点から投入係数および付加価値率を読んでみます。たとえば「第2次産業」ではどうでしょうか。
第2次産業の商品1単位を製造するにあたっては,その生産価額を1とするとき,第1次産業からは0.02,同じ第2次産業からは0.47,サービス他からは0.11の原材料が投入され,それら原材料が生産主体のもとに届けられるにあたり0.09の商業・運輸マージンを要しているあわせて0.69の商品やサービスを投入していることがわかります。
そして,雇用者所得として0.18,営業余剰として0.03,その他として0.10の労働や資本が投入されていることから,あわせて0.31の付加価値が生み出されていることを読みとることができます。
逆行列係数表
上の投入係数表を使って,ここからさらに逆行列係数表をつくっていきたいと思います。
これにあたり,ここでは輸入(地域の場合は移入も)によって波及する分を取り除いて,国内(地域の場合は域内)の波及だけを考慮するモデルを使用することとします。したがって,レオンチェフ逆行列は [I-(I-M)A]-1 型を選択します(各アルファベットは行列をあらわします。具体的に意味するところは後に作成する各表の表題と同じです)。
つづいて,あたらしいシート「~」(注:投入係数表から逆行列係数表までを“つなぐ”という意味で)に,下のように6つの表組みを用意します。
この6つの表は,言い換えれば先のレオンチェフ逆行列を求めるための手順そのものです。
なおこれについても入力が面倒な場合は リンク をクリックであたらしいタブに表組みを開き,それをシート「~」のセルA1にコピーしてもOKです。

ではSTEP1として,「輸入係数」(あるいは移輸入係数)を求めます。
輸入係数は ,各産業について,
中間需要+輸出を除いた最終需要=D
としたときの,Dに占める輸入の割合を意味します。ここでは同じ結果を導ける,より単純な
|輸入|÷(総需要-輸出)
式にて輸入係数を計算したいと思いますが,ここで
- [PDF]平成23年表における調整項の取扱いについて ―"総務省", pp.2-3.
を参照すると,「逆行列係数計算上の扱い」として調整項の扱い方に関する特段の記載があることがわかります。したがって,こちらでもこれにならって
|輸入|÷(総需要-輸出-調整項)
で計算したいと思います。
ということで,「第1次産業」の見出しの右のセルの計算式は
- =ABS('4部門統合表'!N4)/('4部門統合表'!M4-'4部門統合表'!K4-'4部門統合表'!J4)
となります。これを入力後,下方に3セル分コピーしておきます。
![[STEP1]輸入係数](../images/howto/io-table/step31.png)
STEP2,「単位行列I」をつくります。
具体的に,同一産業の交点のセルには「1」,その他のセルには「0」(ゼロ)で埋めます。したがって,下式
- =IF(ROWS($A$9:$A9)=COLUMNS($B$8:B$8), 1, 0)
をセルB9に入力して,表中すべてのセルにコピーします。
![[STEP2]単位行列I](../images/howto/io-table/step32.png)
STEP3,「輸入係数行列M」をつくります。
具体的に,先の「単位行列I」と対応する参照先に1が立っているときのみ,STEP1の輸入係数を転記します。したがって,下式
- =IF(B9=1, $B2, 0)
をセルB16に入力して,表中すべてのセルにコピーします。
![[STEP3]輸入係数行列M](../images/howto/io-table/step33.png)
STEP4,「行列I-M」をつくります。「単位行列I」から「輸入係数行列M」を引いたものなので,これは自給率,つまり
1-輸入率
を意味します。
具体的に,下式
- =B9-B16
をセルB23に入力して,表中すべてのセルにコピーします。
![[STEP4]行列I-M](../images/howto/io-table/step34.png)
STEP5,「行列(I-M)A」をつくります。行列の積なので,Mmult関数を使用します。
具体的には,「第1次産業」の交点のセルから「サービス他」の交点までを選択して,下式を入力します(Mmult関数 ―"Office")。
- =MMULT(B23:E26, '投入係数表A'!C4:F7)
その後,キーボードのCtrlキーとShiftキーを押しながらEnterキーを押し配列数式とします。
![[STEP5]行列(I-M)A](../images/howto/io-table/step35.png)
STEP6,「行列I-(I-M)A」をつくります。
具体的に,下式
- =B9-B30
をセルB37に入力して,表中すべてのセルにコピーします。
![[STEP6]行列I-(I-M)A](../images/howto/io-table/step36.png)
つづいて,あたらしいシート「逆行列係数表」に,下のような表組みを用意します。
なおこれについても入力が面倒な場合は リンク をクリックであたらしいタブに表組みを開き,それをシート「逆行列係数表」のセルA1にコピーしてもOKです。
これは,先のSTEP6表「行列I-(I-M)A」の逆行列ですので,Minverse関数を使用します。
具体的には,「第1次産業」の交点のセルから「サービス他」の交点までを選択して,下式を入力します(Minverse関数 ―"Office")。
- =MINVERSE('~'!B37:E40)
その後,キーボードのCtrlキーとShiftキーを押しながらEnterキーを押し配列数式とします。

「[I-(I-M)A]-1」表・下図・上段の図のハイライトの領域を選択し,オートサム機能で列計を求めます。
同様に「[I-(I-M)A]-1」表・下図・下段の図のハイライトの領域を選択し,オートサム機能で行計を求めます。
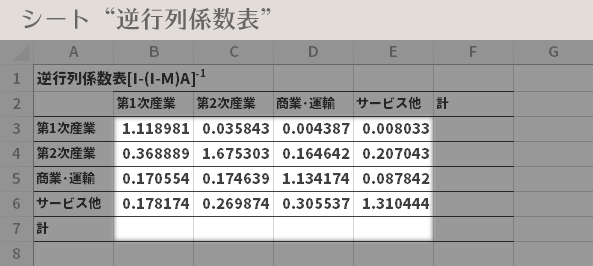
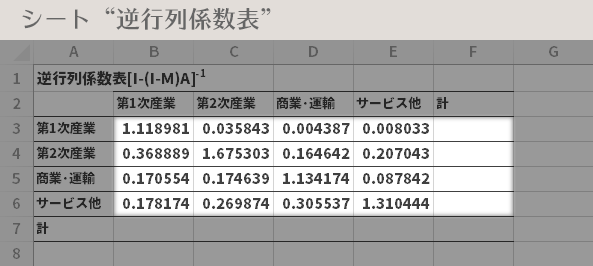
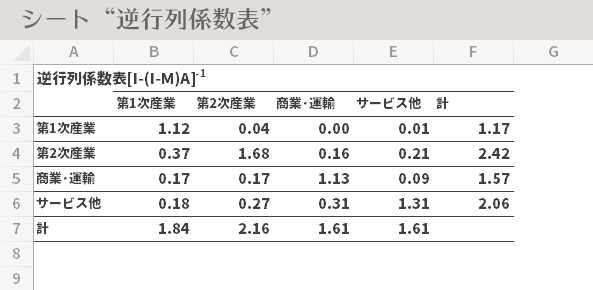
この「[I-(I-M)A]-1」表をタテに見ると,ある部門に1単位の最終需要が生じたとき(直接的な生産の単位),各部門に誘発される生産の大きさ(直接的な生産のもたらす波及効果[=間接的])がわかります。
たとえば「第2次産業」を見てみます。この部門にのみ1単位の最終需要が生じたとき,第1次産業では0.04,第2次産業では1.68,商業・運輸では0.17,サービス他では0.27単位の生産が誘発されることがわかります。つまり,経済全体では2.16単位の生産が生じることが示されます。なお,この表の対角部分(自部門を意味します)の値が1より大きくなっているのは,その直接的な生産単位の1を含むゆえです。
長くなりましたが,以上で4部門統合表・投入係数表・逆行列係数表のすべてが完成です。
影響力係数・感応度係数
少しだけTipsを加えます。
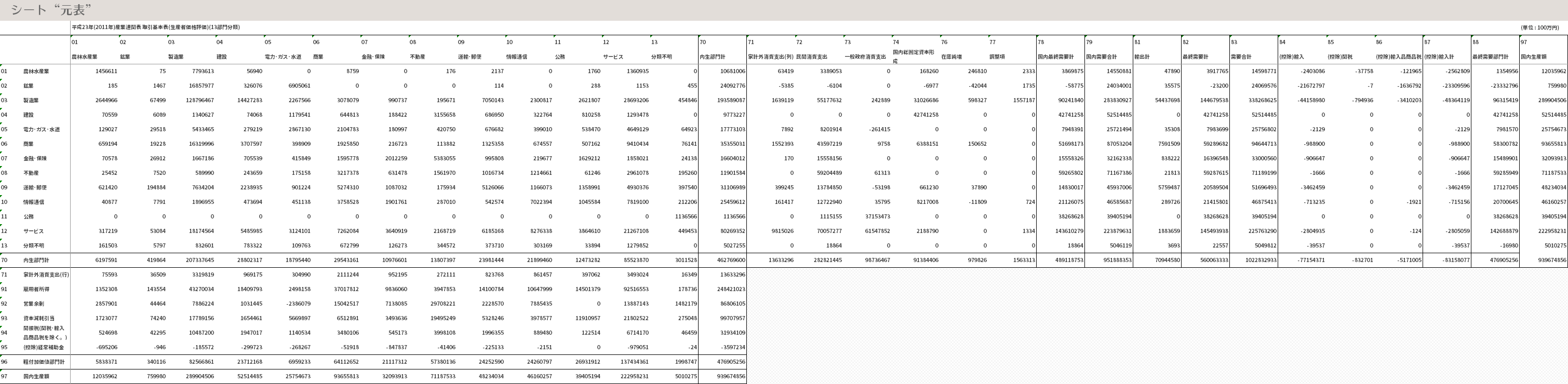
「[I-(I-M)A]-1」表からは,影響力係数(8行)および感応度係数(G列)と呼ばれる係数が求められます。
- CELL B8=B7/AVERAGE($B$7:$E$7)
- CELL G3=F3/AVERAGE($F$3:$F$6)
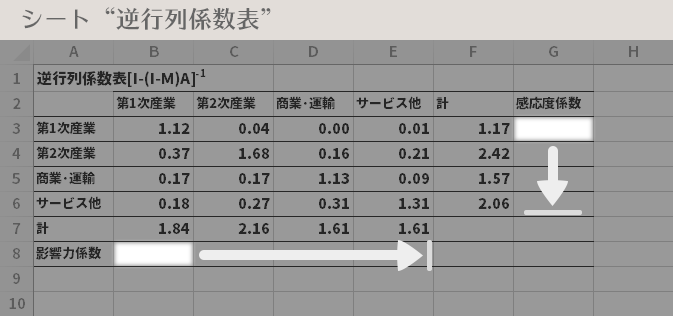
これを計算すると,下の図のような値となります。
本来,4部門統合表のようなきわめて単純化された経済構造のもとでは,影響力係数や感応度係数も漠然としたところを意味するものにすぎなくなってしまいます。ここでは両係数の役割に触れるため便宜上両係数を求めていますが,それぞれの値が具体的に指し示すところは参考程度にとらえてください。
影響力係数は,(見ている)列(の)産業に最終需要が1単位生じたときの波及効果の大きさを相対化(ここでは,平均値を基準に考えるということ)したものです。ここで求めた値では,第2次産業が他の産業から突出(=平均よりかなり大きい)しています。すなわち影響力係数からは,“他の産業をまきこむ力”の多寡がわかります。
感応度係数は,列見出しすべての産業に最終需要が1単位生じたとき,(見ている)行(の)産業に生じる波及効果の大きさを相対化(ここでは,平均値を基準に考えるということ)したものです。同じくここでの値では,第2次産業やサービス他が大きな値(=平均より大きい)となっています。すなわち感応度係数からは,“他の産業に引きずられやすいかどうか”がわかります。