2023/7/10
イントロダクション
経済学のテキストではおなじみな感のあるローレンツ曲線とジニ係数は,所得分配の不平等さを計るための指標です。このような性質から,事務しごとでというよりも,行政組織や公益団体のレポートなどにおいて,いわゆる「所得格差」を検証するためのツールとして用いられているのをよく見かけます。
READ MORE
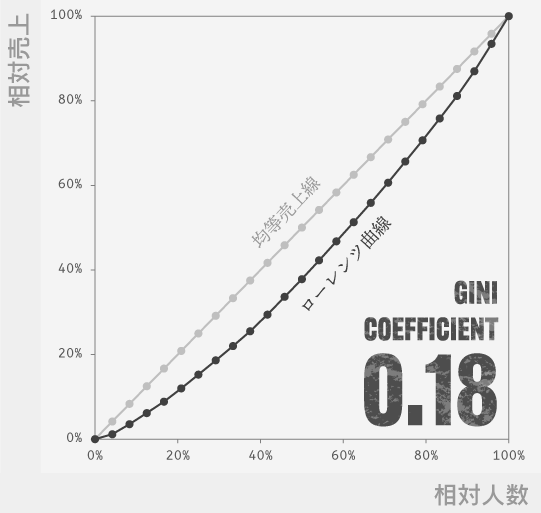
ローレンツ曲線は,横軸に累計の人数,縦軸に所得の累計からなるグラフにプロットされる(曲)線です。所得の小さな人から順番に積み上げるという決まりのもと,所得の累積値と人数の累積値との関連から(曲)線の特徴が定まっていきます。もっとも,すべての国民の所得のように人の数(つまり項目値)が膨大となる場合,一般的には全体をいくつかに等分した要約値が用いられることが多いです。
ジニ係数は,ローレンツ曲線から計算される値です。もし,すべての人がまったく同じ所得であると仮定すると,ローレンツ曲線は一定の傾きをもつことになります。仮にこの条件を満たす線を「均等所得線」と呼ぶものとします。ローレンツ曲線がこの均等所得線と一致することを「格差が存在しない」状態と定めるなら,転じて格差が存在する状態では傾きが一定ではなくなる,ということになります。ごく限られた一部の人だけに富が集中する状態では,ローレンツ曲線は右下方に大きくふくらんだ(凸)ような形となります。ジニ係数は,ここでいう「格差が存在する」状態のローレンツ曲線と「格差が存在しない」状態のローレンツ曲線(均等所得線)」を含むグラフ上の領域の面積を除して計算します。
このとき「格差が存在しない」状態ではジニ係数は0に,「格差が存在する」状態ではその程度が大きいほど1に近づいていくことになります(ただしこのページの方法では完全に1になることはありません)。
ただ,この数字をどう判断するかについては,「格差とは」の定義が必要となるでしょう。このサイトでは手の届かない議論ですので,その点は踏み込んでおりません。
ここでは,ローレンツ曲線とジニ係数を「所得格差」でなく販売担当部員に見る売上のばらつき,いうなれば会社の中での「営業力差異」を異なる時点間で比べてみよう,といった趣旨で使用します。当然メインストリームからは外れますので、結論としては参考レベルを超えない範囲で利用することを想定しています。この点含みおきください。
以下,Excelによるローレンツ曲線の描き方・ジニ係数の計算方法です。ここでは一連の手続きをサブスクリプション版Excel(ver.2007)で追っています。一部ボタンの配置や名称などが異なる箇所がありますが,手続きそのものは「永続ライセンス版」にいうところのExcel 2019, 2016, 2013, 2010も基本的に同じです。
なお,下のスイッチで新機能「スピル」に沿った説明に切り替えが可能です(デフォルト:OFF)。

元データ
元のデータです。
この年6月の販売担当部員の売上を集計したものです(単位:円)。

小さな値から順に並べる
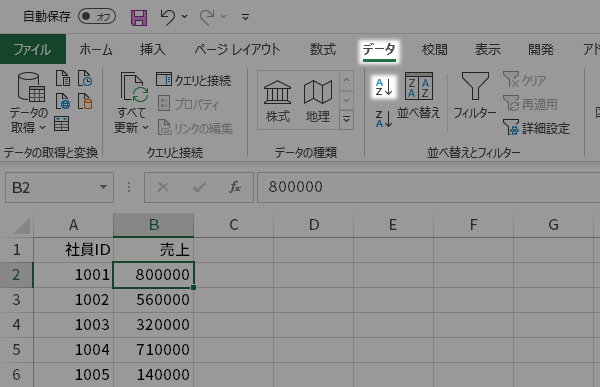
「売上」データの昇順に並べ替えます。「売上」の任意のデータを選択し

リボンのデータタブ並べ替えとフィルタグループにある昇順ボタンをクリックします。
これによりデータが昇順に並べ替えられます。
表の基部をつくる
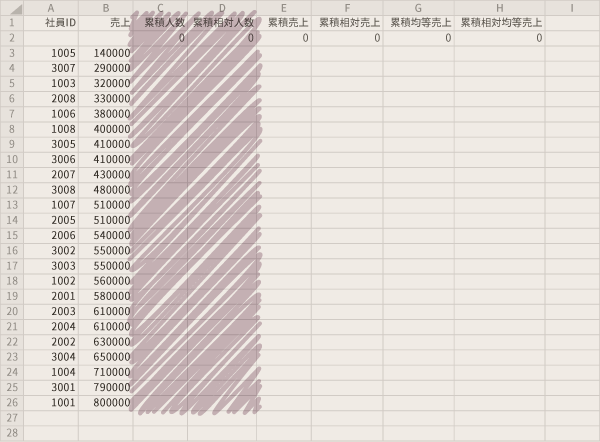
あたらしく見出しを追加します。
ここではセルC1から向かって右に累積人数累積相対人数累積売上累積相対売上累積均等売上累積相対均等売上の順に6個作成しています。
![[セルC1]累積人数,[セルD1]累積相対人数,[セルE1]累積売上高,[セルF1]累積相対売上高,[セルG1]累積均等売上高,[セルH1]累積相対均等売上高](../images/howto/lc-gc/step4-1@1x.png)
見出しとデータの間にあたらしい行を挿入します。
つづいて,この行の「累積人数」から「累積相対均等売上」列のすべてに0(ゼロ)を入力していきます。
ここで0を挿入する理由はローレンツ曲線を原点から引くためです。
![行の挿入後,[セルC2:H2]0](../images/howto/lc-gc/step5-1@1x.png)
「人の数」を積み上げる
では,最初にこの強調部分を作成していきます。ここで「累積相対人数」は,“人の数”に関して,当該行時点での累積値の全体に占める割合を示すものです。
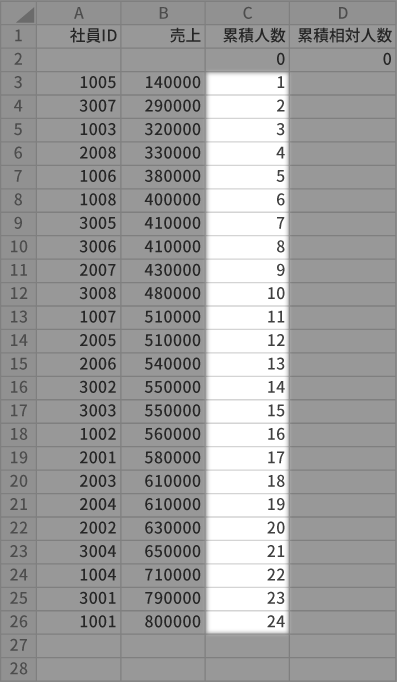
「累積人数」列にリストの24人分の値を連続データで作っていきます。
- CELL C3=SEQUENCE(24, 1)
「累積相対人数」列について,
累積人数÷総人数
となる式を配置します。具体的には,セルD3に
- CELL D3=C3/\$C\$26
- CELL D3=C3#/C26
と入力します。このとき,「総人数」にあたるセル(ここではC26)はコピーすることを考慮して絶対参照としておきます。
この式を表の最下行までコピーし,ついでにパーセントスタイルを適用します。
と入力します。あわせてこの列にパーセントスタイルを適用しておきます。
![[セルD3]=C3/$C$26。この式をセルD26までコピー](../images/howto/lc-gc/step8-1@1x.png)
![[セルD3]=C3#/C26](../images/howto/lc-gc/step8-1-spill@1x.png)
「金額」を積み上げる
続いてはこの強調部分を作成していきます。ここで「累積相対売上」は,“売上”に関して,当該行時点での累積値の全体に占める割合を示すものです。
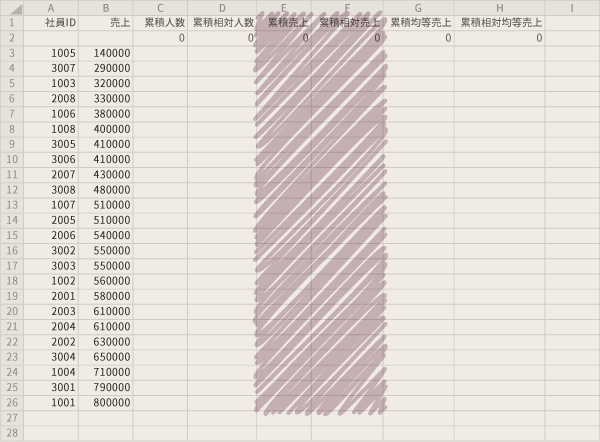
「累積売上」列について,先頭行のみ「売上」の先頭データを参照する式を,次行以降は
直前の累積売上+当該行の売上
となる式を配置します。具体的には,セルE3に
- CELL E3=B3
と,セルE4に
- CELL E4=E3+B4
と入力します。
これらを入力したのち,E4の計算式だけを表の最下行までコピーします。
Excelについてある程度の練度にあれば,CELL E3=SUM(\$B\$3:B3) を最下行までコピーした方がスマートです。
![[セルE3]=B3, [セルE4]=E3+B4。セルE4の式をセルE26までコピー](../images/howto/lc-gc/step10-1@1x.png)
「累積相対売上」列について,
当該行の累積売上÷総売上
となる式を構成します。具体的には,セルF3に
- CELL F3=E3/\$E\$26
- CELL F3=E3:E26/E26
と入力します。
この式を表の最下行までコピーし,あわせてパーセントスタイルを適用しておきます。
と入力します。あわせてこの列にパーセントスタイルを適用しておきます。
![[セルF3]=E3/$E$26。この式をセルF26までコピー](../images/howto/lc-gc/step11-1@1x.png)
![[セルF3]=E3:E26/E26](../images/howto/lc-gc/step11-1-spill@1x.png)
差はないと仮定して再度「金額」を積み上げる
今度はこの強調部分を作成していきます。この部分は「均等所得線」「均等分配線」などと呼ばれる,一定の傾き(グラフが正方の場合は45°)をもつ直線をグラフに描画するために用います。ここでは,さしずめ「均等売上線」とでも呼んでおこうと思います。
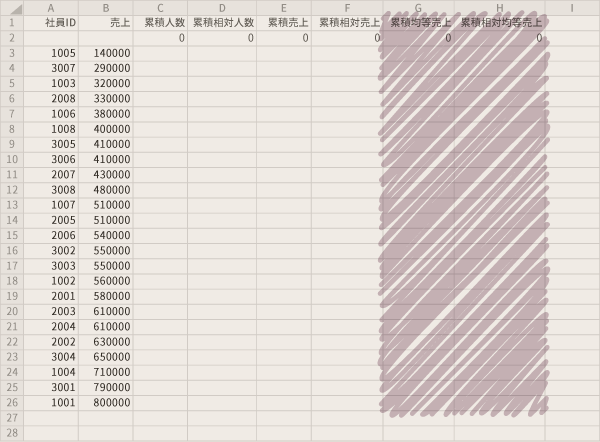
「累積均等売上」列について,総売上から1人当たりの売上を求め(平均売上),これを累積値として表示します。したがって,
総売上÷総人数×当該行の累積人数
となる式で計算します。具体的には,セルG3に
- CELL G3=\$E\$26/\$C\$26*C3
- CELL G3=E26/C26*C3#
と入力します。
この式を表の最下行までコピーします。
![[セルG3]=$E$26/$C$26*C3。この式をセルG26までコピー](../images/howto/lc-gc/step13-1@1x.png)
![[セルG3]=E26/C26*C3#](../images/howto/lc-gc/step13-1-spill@1x.png)
「累積相対均等売上」列について,
当該行の累積均等売上÷総売上
となる式を配置します。具体的には,セルH3に
- CELL H3=G3/\$G\$26
- CELL H3=G3#/G26
と入力します。
この式を表の最下行までコピーし,加えてパーセントスタイルを適用しておきます。このとき,「累積相対均等売上」列の値そのものは「累積相対人数」列のそれと一致するはずです。
と入力します。あわせてこの列にパーセントスタイルを適用しておきます。
このとき,「累積相対均等売上」列の値そのものは「累積相対人数」列のそれと一致するはずです。
![[セルH3]=G3/$G$26。この式をセルH26までコピー](../images/howto/lc-gc/step14-1@1x.png)
![[セルH3]=G3#/G26](../images/howto/lc-gc/step14-1-spill@1x.png)
「散布図」を使ってローレンツ曲線その他を図示する
ではこの表をもとに,ローレンツ曲線と均等売上線からなるグラフを作成します。
グラフ化に必要なデータは「累積相対人数」列,「累積相対売上」列,および「累積相対均等売上」列の3つです。
したがって下のハイライトの領域を選択しておきます。
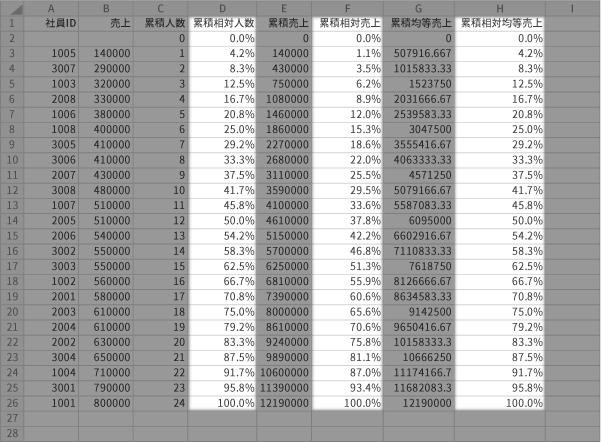
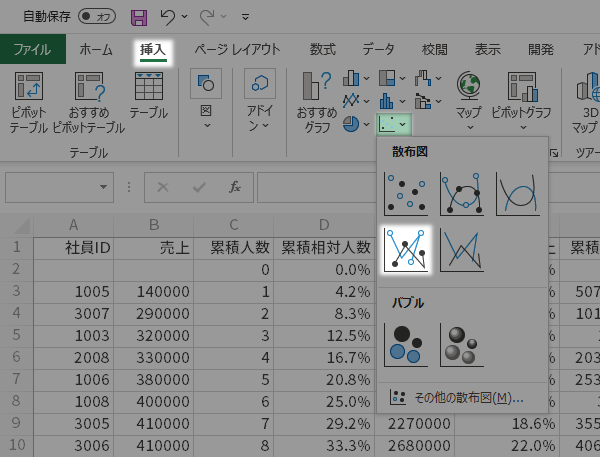
リボンの挿入タブグラフグループにある散布図(X, Y)またはバブルチャートの挿入ボタンをクリックします。
つづいて,プルダウンから散布図(直線とマーカー)ボタンを選択します。
DIFFERENT VERSIONS
2010: 挿入タブグラフグループにある散布図ボタン
グラフが作成されました。
ここでグラフの横軸は「相対人数(人数の累積比)」を,縦軸は「相対売上(売上の累積比)」をあらわしています。ここでいう青線がローレンツ曲線,オレンジの線が均等売上線です。
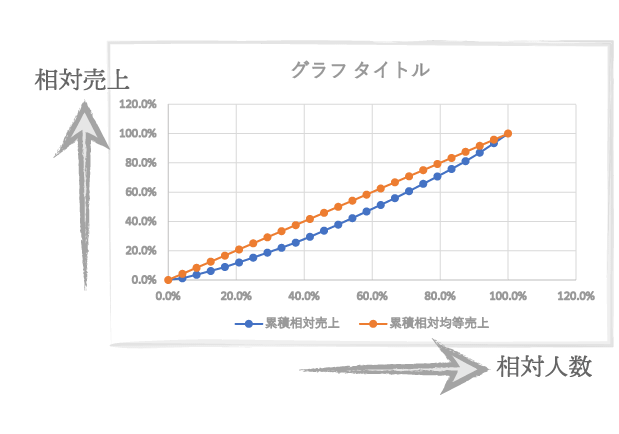
グラフを任意に調整していきます。
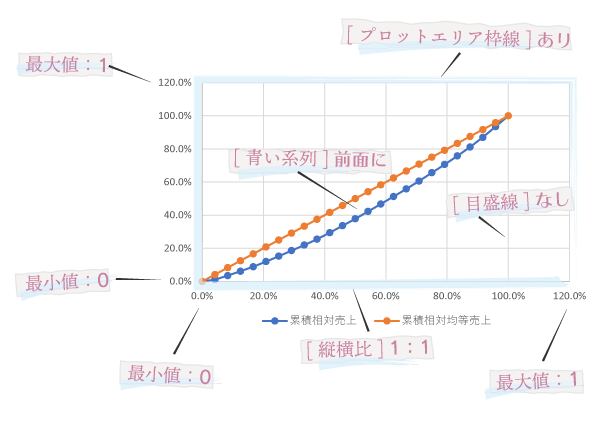
ここでは,主に下の図のような数個の点について設定を加えることにしました。
- 縦・横軸とも最小値 0,最大値 1
- プロットエリア 枠線を作成,目盛線削除,できるだけ正方に
- 両軸の表示形式 (現状を確認して,未適用なら)パーセント
なお,この場合のグラフの“主役”がローレンツ曲線であることを慮れば,さらなる手数を費やせるなら望ましいだろうなーと私が思う処理として,参考までに
- 系列「累積相対売上」を最前面に移動(系列の順序設定)
を加えておきます。

「図形の面積」について考える
次はグラフの中の2つの図形に注目してみたいと思います。
これ と これ です。
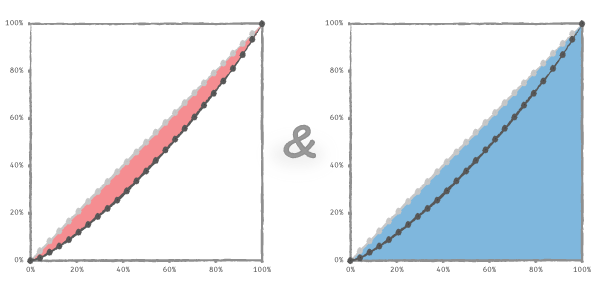
ジニ係数は上の図の
赤の面積÷青の面積
で求めることができます。
全体を1としたとき(タテ100%× ヨコ100%= 1),青の面積はその半分なので0.5というのはすぐ分かるのですが,赤の面積はちょっと悩みますね。

あと,ええと,参考としてですけど青の面積が0.5という点に着目すれば,ジニ係数は下の式でも計算できることがわかります。
上の式(赤の面積÷青の面積)の分子分母にそれぞれ2を掛けてやると,ジニ係数は赤の面積の2倍と等くなることが示されます。ということで,下の式でもOKなワケですが,ここでは先に上で示した方の式を使用していきたいと思います。
![[参考]ジニ係数=2*赤の面積](../images/howto/lc-gc/step21-1@1x.png)
いずれの方法にしろ,赤の面積を知る必要があります。とはいえ,赤の面積を直接計算するのはややこしそうです。
したがって,ここでは赤の面積を下の図のような手続きで計算することとします。
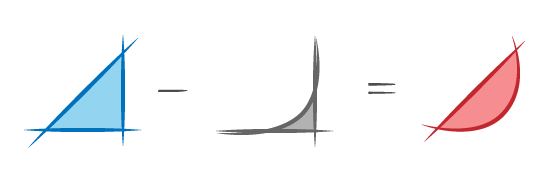
この最初の三角形の面積は0.5だと分かってますので,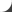 部分の面積が計算できればOKというわけです。
部分の面積が計算できればOKというわけです。
となれば, 部分(ローレンツ曲線下方)の面積の計算方法についてあらかじめ練っておきたいと思います。
部分(ローレンツ曲線下方)の面積の計算方法についてあらかじめ練っておきたいと思います。
ローレンツ曲線下方の領域は,下の図のような,たくさんの台形に分解して考えることができます。そこでこの領域の面積は,1つ1つの台形の面積を求め,合算するという方法なら計算できることがわかります(cf. 積分)。
より忠実には,グラフにいう左端の「台形」は三角形です。
その1つ1つの台形の面積ですが台形の面積を求めるための公式は,よく知られた
- (上底+下底)×高さ÷2
です。
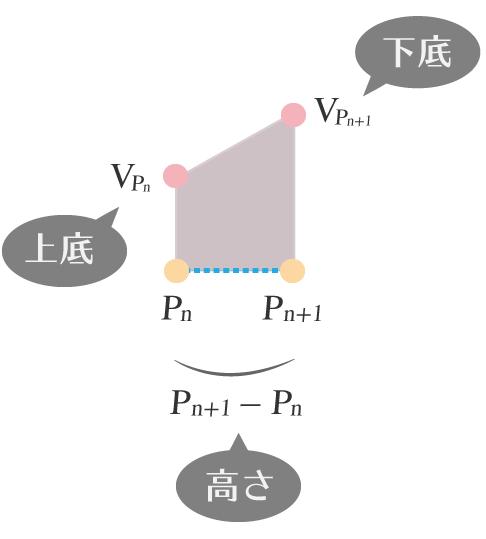
そこで公式の各要素を,ここで扱う台形に下の図のようにあてはめてみたいと思います。

台形の青い破線部,すなわち相対人数をあらわす横軸について,左下の角を$P_n$,右下の角を$P_{n+1}$としたとき,$P_n$,$P_{n+1}$と対応する相対売上をそれぞれ$V_{P_n}$,$V_{P_{n+1}}$とします。
このとき,先の公式の各要素との対応は次のようになります。
[上底] $V_{P_n}$
[下底] $V_{P_{n+1}}$
[高さ] $P_{n+1}-P_{n}$
ジニ係数を求める
そういったことを心に留め置きつつ,ふたたび元の表の方に視点を移します。
表の右に,あたらしい見出しとなる台形の面積を用意します。
さらに,この見出しの直下のセルに0(ゼロ)を入力しておきます。
![[セルI1]台形の面積, [セルI2]0](../images/howto/lc-gc/step27-1@1x.png)
公式に当てはまるよう計算式を組み立てます。
具体的には,セルI3に
- CELL I3=(F2+F3)*(D3-D2)/2
と入力します。
入力できたらこれを表の最下行までコピーします。
![[セルI3]=(F2+F3)*(D3-D2)/2。この式をセルI26までコピー](../images/howto/lc-gc/step28-1@1x.png)
個々の台形の面積を合計すると,下のような結果となります。
これが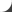 部分(ローレンツ曲線下方)の面積ということになります。
部分(ローレンツ曲線下方)の面積ということになります。
ということで,赤の面積は0.5-0.41=0.09と計算できました。

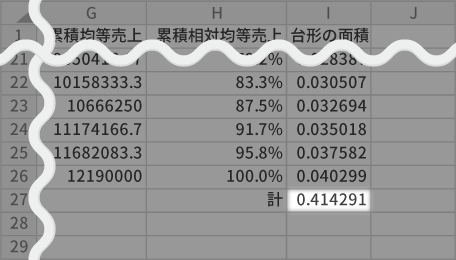
そしてジニ係数は「赤の面積÷青の面積」でしたので
0.09÷0.5=0.18と求められます。
ローレンツ曲線のグラフの描画,およびジニ係数の計算,完了です。