Excelによる、母比率の検定。

OSS社から依頼の調査のひとつに，サービスの認知に関する調査'task C'があります(標本のサイズ$n$: 300)。

具体的には，OSS社がターゲットと定義するクラスタ(企業および団体)を対象にした，「オフィス向けに据え置き菓子を提供するサービスの業態」が存在することがどの程度認知されているかの調査です。

先輩の話によると，OSS社はおよそ3年前，同様の調査を他社に依頼し，より大規模におこなっているようです。そのときの認知率［標本比率］は22.0%であったとのことでした。ここではこの値を比較値($p_0$)として考えます。

下が今回の調査で集まったデータです。なお「区分」系列はカテゴリデータで，1が「認知している」状態を，0が「認知していない」状態をあらわしています。

僕は，これらについて統計的検定をおこなうよう先輩から指示を受けました(両側，有意水準 5%。ワードについては別頁)。以下，このtaskについて検定をおこないます。

先んじて立てておいた仮説は次のとおりです。ここでは帰無仮説として「母比率は比較値と一致している」ことを立て，対立仮説としては「母比率は比較値と一致していない」ことを立てました(両側検定)。

帰無仮説は「このデータは 認知率を$p_0$とする母集団から抽出されたものである」ことを，対立仮説は「認知率を$p_0$とする母集団から抽出されたものでない」ことを示しています。つまり帰無仮説が棄却されれば，3年前と現在の認知率の差は有意なものと考えることができます。

ここから検定統計量を計算していきます。

比率YesかNo(=Yesでない)のような2つの項目から一者が選択された割合に関する検定は，原則的には文字通り二項分布の守備範囲ではあります。二項分布は 試行回数$n$，成功確率$p$を母数とする離散分布です。ここで二項分布の確率変数つまり成功回数を$x$とすると，$x$の平均は$np$，分散は$np(1-p)$によって求められます。

二項分布はうれしい？ことに，ここでのtaskのように$n$がある程度大きな場合は，$x$を正規分布で代替して考えることができるようになります(近似する)。

これは標本比率つまり$x/n$についても同様で，先の式よりこのときの正規分布の母数は，平均$np/n=p$，分散$(np(1-p))/n^2=p(1-p)/n$となることが予見できます。したがって$p$を帰無仮説が正しいと仮定したときの母比率$p_0$とし，また$x/n$を $\hat{p}$ と定義するとき，平均$p_0$，分散$p_0(1-p_0)/n$の正規分布にあって，観測された $\hat{p}$ がどれだけ突飛かを計ればよいことが分かります。

ただしこれは母平均の検定のときと同じように，考え方としては$z$(標準正規)分布が使えるよう標準化したほうがスッキリ/スマートなことから，下式のとおり標準化して，これを検定統計量として用いていきます(以下，検定統計量については一律 $T$ であらわします)。

$T$を求めるため，必要なデータをシートに用意していきます。

まずは「(標本の)サイズ$n$」と「比較値$p_0$」(ここでは過去調査の認知率)です。

“認知している”状態に関して，「標本比率$\hat{p}$ 」を求めます。

この例ではカテゴリ'1'の個数をカウントし，$n$で割って計算したいと思います。

$T$を計算します。ここでは分子と分母に分けて計算しています。

あらかじめ決めておいたor指定された「有意水準$α$」を設定します。今回，先輩から有意水準は5%にする旨指示されていますので，ここは0.05とタイプしました。

1. 【方法1】$T$と 棄却限界値 を比較する すぐ下の手続きから
2. 【方法2】$P$値と 有意水準 を比較する 13 へ

【方法1】棄却限界値を求めます(ここでは右側のそれを求めています)。片側検定の場合の値も計算していますが，task Cは両側検定なのであくまで参考としての掲示です。

• “両側”の計算式
• =NORM.S.INV(1-E12/2)

• “片側”の計算式
• =NORM.S.INV(1-E12)

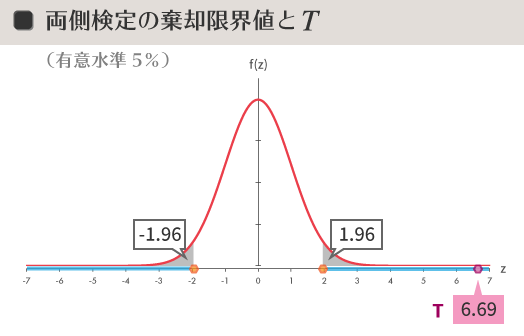
棄却限界値は1.96とわかりました。

ということは，下の図のように$T$の値(6.69)は棄却域(淡い空色の線)にかかります。

【方法2】$P$ 値(有意確率)を求めます。

ここでは両側検定の$P$ 値は片側検定の$P$ 値を2倍して求めたいと思います。具体的には，下図のようにいったん「片側」の$P$ 値を求めて，その値を「両側」で参照する構造をとっています。もちろんセルE15のみで片側の2倍を計算してもOKです。

• “片側”の計算式
• =1-NORM.S.DIST(ABS(E10), TRUE)

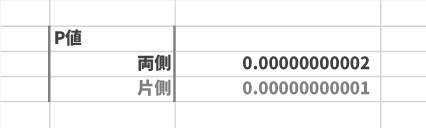
$P$ 値 は「両側」で0.00000000002となりました(なお値が小さすぎるので通常は指数表記［2.23268E-11 など］で表示されるかと思います)。

以上のとおり，方法1では

• T > 棄却限界値

となり，方法2では

• $P$ 値 < 有意水準$α$

となりました。

いずれにしろ標本比率$\hat{p}$ と比較値$p_0$との差(16%)について，「帰無仮説の下ではめったに起きないことが起きた」つまり，そもそもの仮説が間違っていたと考えます。

よって帰無仮説を棄却し，対立仮説を採択“確率的に意味のある差であった” と判断します。