Excelによる、母分散の検定。

ダブルタワーに入居する高級中華料理店「○○苑」の代表的なコース料理“A”は，固有のアルゴリズムが組み込まれた“システム”によって料理を提供するタイミングを決定しています。

この“システム”の導入の際，設備・動線・人員等設計の面からもあわせて最適化が施されました。しかし，店のアナウンスによると実際の運用にあたってはどうしても“システム”がはじき出した好適なタイミングからは60秒程度のずれが出てしまうようです(ただし母平均は未知と仮定)。

実際にデータをとってこのずれを確認したものが次の表です(無作為抽出と仮定)。

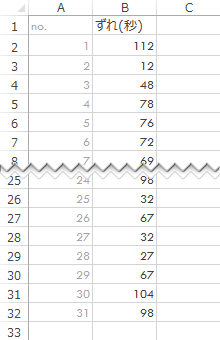
上表から平均を求めてみると，およそ62秒となり店のアナウンスと有意な差はありません。が，いかんせん，平均が許容値にあるかどうかにすべての意識を奪われて，“バラツキ”具合の方を管理できていなかったとしたら，好適なタイミングを実現することを目的として動いているはずの“システム”の意義が薄まってしまいます。

したがってこの店では，これを分散900秒²(標準偏差30秒)でコントロールしているということです。

ということで，今度は不偏分散をもとめてみると，およそ700秒²(標準偏差にしておよそ26 秒)となり，あいまいな感覚的のもとではアナウンスに言うコントロール(比較値$\sigma^2_0$: 900秒²)のもとにありそうな気もなさそうな気もします。

そこでここでは，実のところ母分散は900秒²じゃない(=アナウンスと異なる)のでは？言い方を換えれば$\sigma^2\neq\sigma^2_0$が言えるかどうかの検定をしてみようと思います。

以下，このタスクに関する検定の手続きです(両側, 有意水準5%。ワードについては別頁)。

では，ここから検定のプロセスです。

最初に立てておいた仮説は次のとおりです。ここでは帰無仮説として「母分散は比較値と一致している」ことを立て，対立仮説としては「母分散は比較値と一致していない」ことを立てました(両側検定)。

この帰無仮説は「このデータは，分散＝900秒²の母集団から抽出されたものである」ことを，対立仮説は「それとは異なる母集団から抽出されたものである」ことを言っています。つまり帰無仮説が棄却されれば，店側のアナウンスの裏付けが弱くなります。

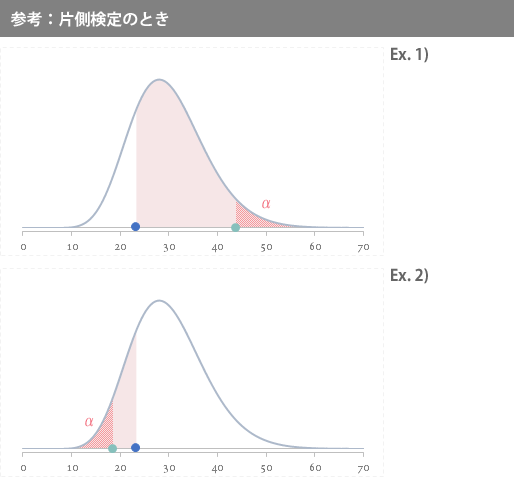
また参考として，片側検定の場合は次のような仮説が考えられます。

下図の仮説 Ex.1)は「母分散が900秒²より大きい」ことを，Ex.2)は同じく「900秒²より小さい」ことを主張する場合の設定です。

では，ここより必要な入力をおこなっていきます。

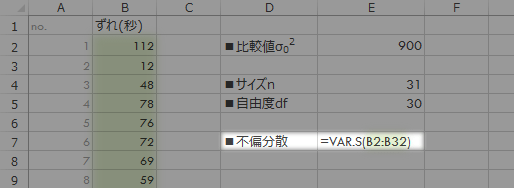
まずは「比較値」($\sigma^2_0$: ここではアナウンスされた値→900秒²)です。

つづいてサンプルサイズと自由度を入力ないし計算します。

• CELL E4=COUNT(B2:B32)
• CELL E5=E4-1

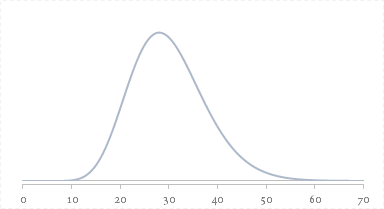
ちなみに，この自由度30の$\chi^2$分布は下の図のような形状となります。

5 で触れた不偏分散をあらためて正しく計算しなおします。

• =VAR.S(B2:B32)

検定統計量(帰無仮説が正しいとしたときの$\chi^2$値)を計算します。式は次のとおりです(以下，検定統計量についてこのページでは一律 $T$ であらわします)。

この例のようにダイレクトに偏差平方和(DEVSQ)を計算可能なシート構成を用意する場合，分子はそちらに代えてもOKです。

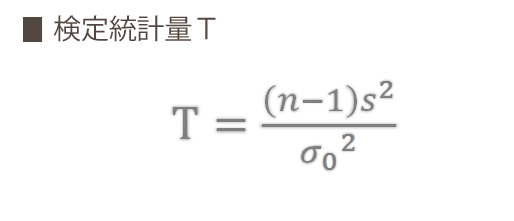
• $n-1$: 自由度
• $s^2$: 不偏分散
• $\sigma^2_0$: 比較値

なおここでは，T の計算にあたり上の式の分子と分母にわけて計算するものとします。

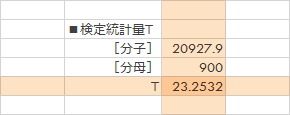
• CELL E10: 分子=E5*E7
• CELL E11: 分母=E2
• CELL E12: T=E10/E11

$T$は23.25となりました。

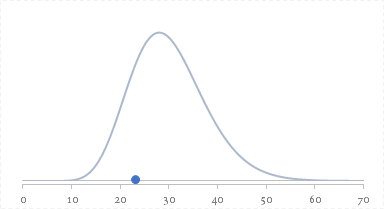
これを先ほどの$\chi^2$分布($df$=30)のグラフにプロットすると，次のようになります。横軸青色の点が$T$です。

有意水準($α$)を入力します。5 の設定のとおり，ここでは0.05(5%)とします。

以降の手続きは分岐します。次のいずれかの判定法を選択して進めます。

1. $T$と 棄却限界値 の比較による方法 すぐ下の手続きから
2. $P$値と 有意水準 の比較による方法 24 へ

ここでは棄却限界値をもとめます。

• “上側”の計算式
• =CHISQ.INV.RT(E14/2, E5)

• “下側”の計算式
• =CHISQ.INV.RT(1-E14/2, E5)

上側の棄却限界値は46.98，下側のそれは16.79という値が返ってきました。

またまた参考に片側検定の場合の棄却限界値も求めてみます。

上側の棄却限界値(仮説 Ex.1 の場合に利用)と下側のそれ(仮説 Ex.2 の場合に利用)は，それぞれ次式で求めます。

• “上側”の計算式［片側検定］
• =CHISQ.INV.RT(E14, E5)

• “下側”の計算式［片側検定］
• =CHISQ.INV.RT(1-E14, E5)

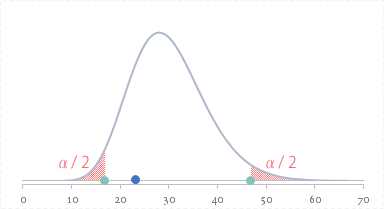
ここで 18 の数字(両側検定の場合の棄却限界値)をグラフに図示してみると横軸上の緑色の点になります(下図)。

19 の数字(片側検定の場合の棄却限界値)も同じくグラフに図示すると次のようにあらわすことができます(下図)。

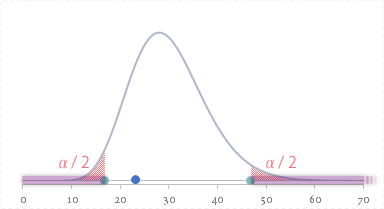
ということで，$T$(青色の点)は棄却域(下の図でいう横軸上の紫色の領域)にはかからないことがわかります。

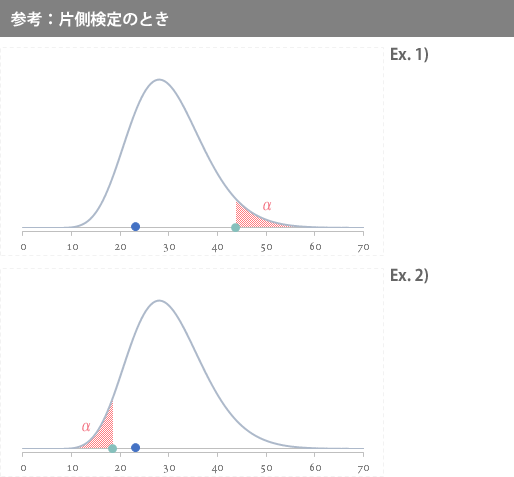
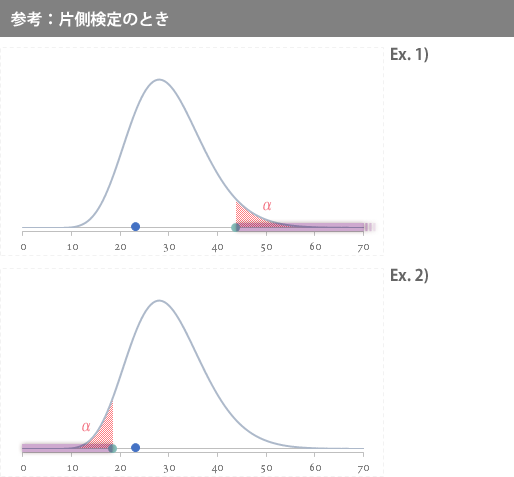
なお参考として，片側検定の場合には，両者の位置関係は下の2番目の図のとおりです。

したがって両側検定の場合，不偏分散($s^2$)と比較値($\sigma^2_0$: 900)との差について，「帰無仮説の下ではめったに起きないことが起きた」ゆえとまでは言えません。

よって帰無仮説は棄却せず，「確率的に意味のある差ではなかった」と判断します(検定了)。

ここでは$P$ 値をもとめます。

$\chi^2$検定では左右に非対称な分布を扱うことから，両側検定の場合は$T$により近い上下いずれかの棄却限界値の側で確率を計算し，これを2倍して$P$ 値を求めます。

具体的な方法のひとつとして，まず，次式で$T$から上下両方向に対しての確率を求めます。

• 上側確率
• =CHISQ.DIST.RT(E12, E5)

• 下側確率
• =1-E23

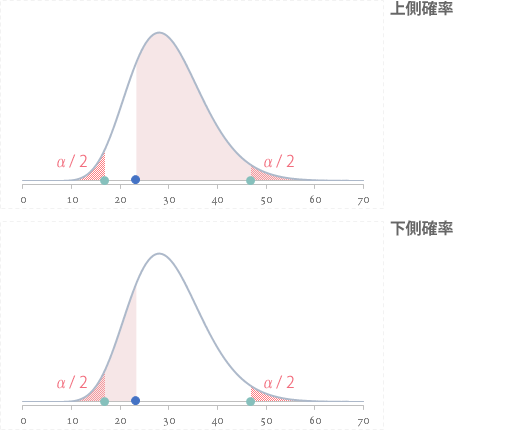
片側検定の場合，直前の 24 のそれぞれの値が$P$ 値となります(仮説 Ex.1 では「上側」を，Ex.2 では「下側」を利用)。

これらの値は，下図の淡いピンク色の領域で示されます(赤いハッチングの領域［有意水準］と重なる部分あり)。

また両側検定の場合は下のように図示できます。

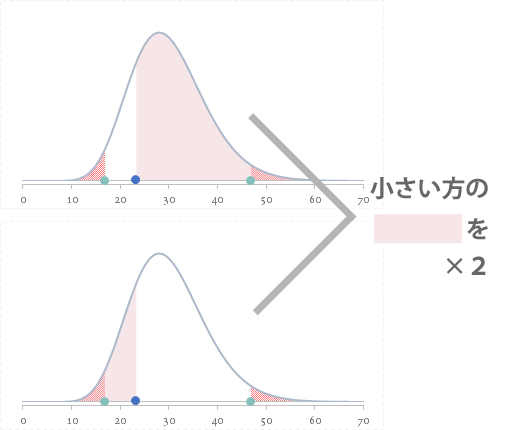
両側検定にあっては，これら「上側」または「下側」いずれかの値の小さな方を2倍して$P$ 値をもとめます。

• 両側確率
• =MIN(E23:E24)*2

$P$ 値は0.39と返りました。

結果，$P$ 値(39%)は有意水準(5%)より大きいことがわかりました。したがって両側検定の場合，不偏分散($s^2$)と比較値($σ^2_0$)との差について，「帰無仮説の下ではめったに起きないことが起きた」ゆえとまでは言えません。

よって帰無仮説は棄却せず，「確率的に意味のある差ではなかった」と判断します(検定了)。